Решение на системата от уравнения в Microsoft Excel

Способността да се решават системи от уравнения често могат да се възползват не само от ученето, но и на практика. В същото време не всеки потребител на компютър знае, че има собствени варианти за решаване на линейни уравнения в Excel. Нека да разберем как да изпълняваме тази задача, като използваме различни инструменти на този процесор по различни начини.

варианти за решение

Всяко уравнение може да се счита за разрешено само когато се открият неговите корени. В Excel има няколко възможности за намиране на корените. Нека да разгледаме всеки от тях.

Метод 1: Матричният метод

Най-честият начин за решаване на система от линейни уравнения с инструменти на Excel е да се използва матричен метод. Състои се в изграждането на матрица от коефициенти на изразяване и след това в създаването на обратна матрица. Нека се опитаме да използваме този метод, за да решим следната система от уравнения:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


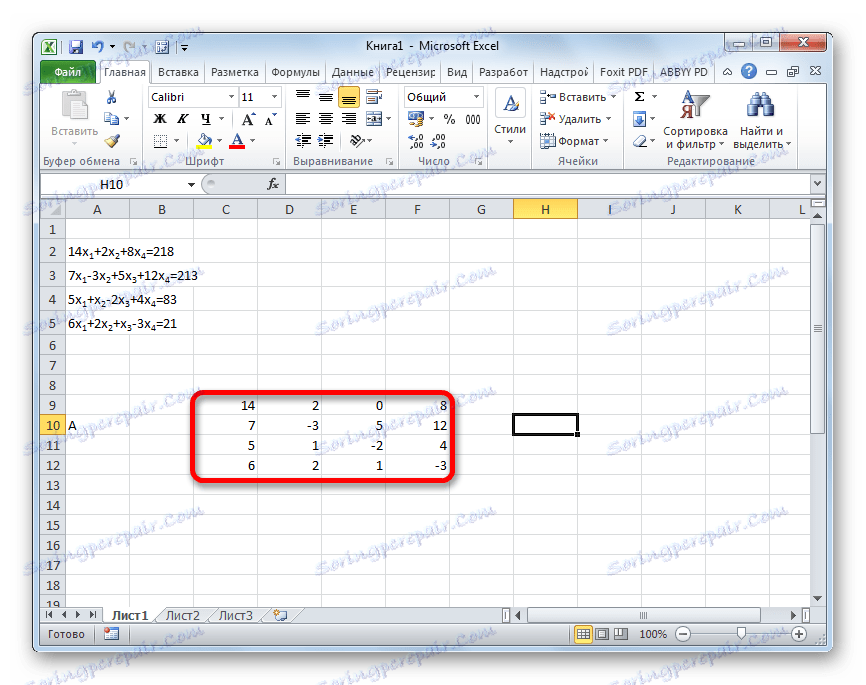
1. Запълваме матрицата с числа, които са коефициенти на уравнението. Тези номера трябва да бъдат подредени последователно, като се вземе предвид местоположението на всеки корен, към който отговарят. Ако в един израз липсва един от корени, тогава в този случай коефициентът се счита за равен на нула. Ако коефициентът не е посочен в уравнението, но съответният корен е налице, тогава се приема, че коефициентът е 1 . Ние обозначаваме получената таблица като вектор А.
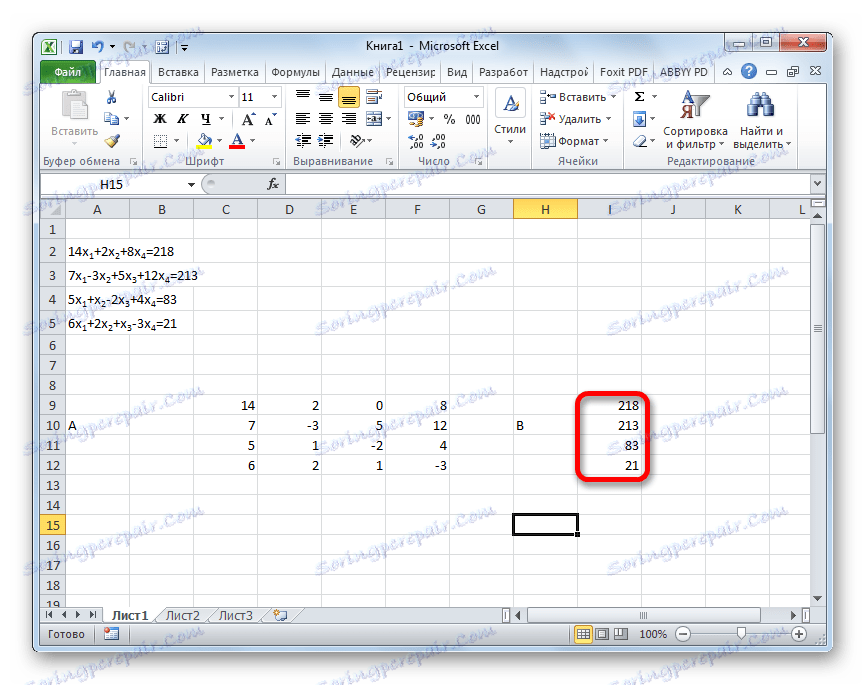
2. Отпечатайте отделно стойностите след знака "се равнява на". Обозначете ги с общото им име, като вектор В.
3. На първо място, за да открием корените на уравнението, трябва да намерим обратната матрица на съществуващата. За щастие, Excel има специален оператор, който е предназначен да реши този проблем. Тя се нарича ICBM . Той има сравнително прост синтаксис:

   =МОБР(массив)

   Аргументът "Array" е всъщност адреса на таблицата източник.

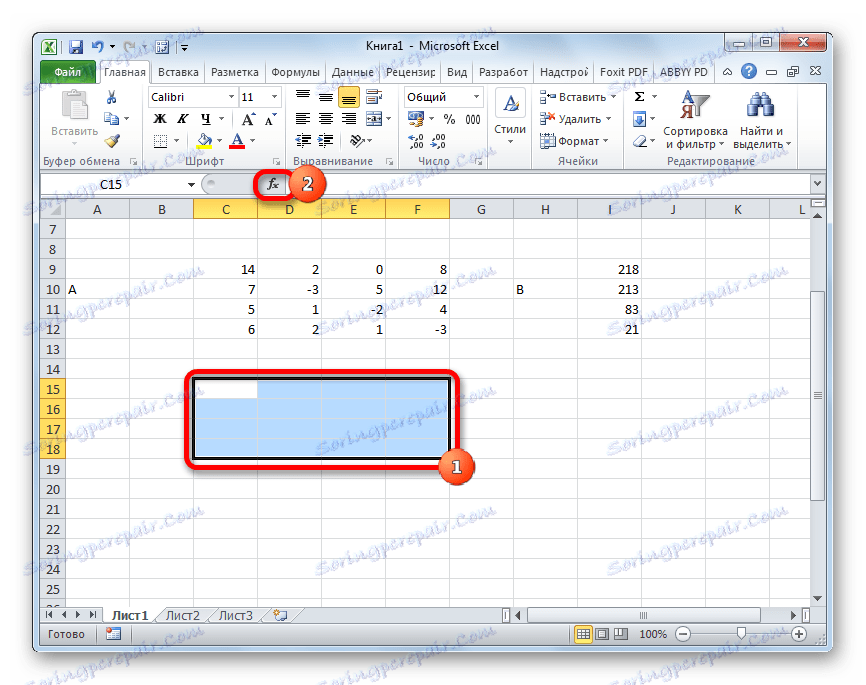
   Така че, нека изберете област от празни клетки на листа, която е равна на размера на оригиналната матрица. Кликваме върху бутона "Вмъкване на функция" , разположен близо до формулата.

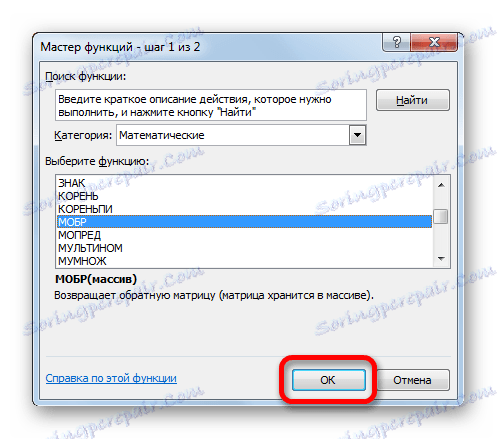
4. Стартира съветникът за функции . Да отидем в категорията "Математически" . В представения списък търсим името "MOBR" . След като го намерите, изберете го и кликнете върху бутона "OK" .
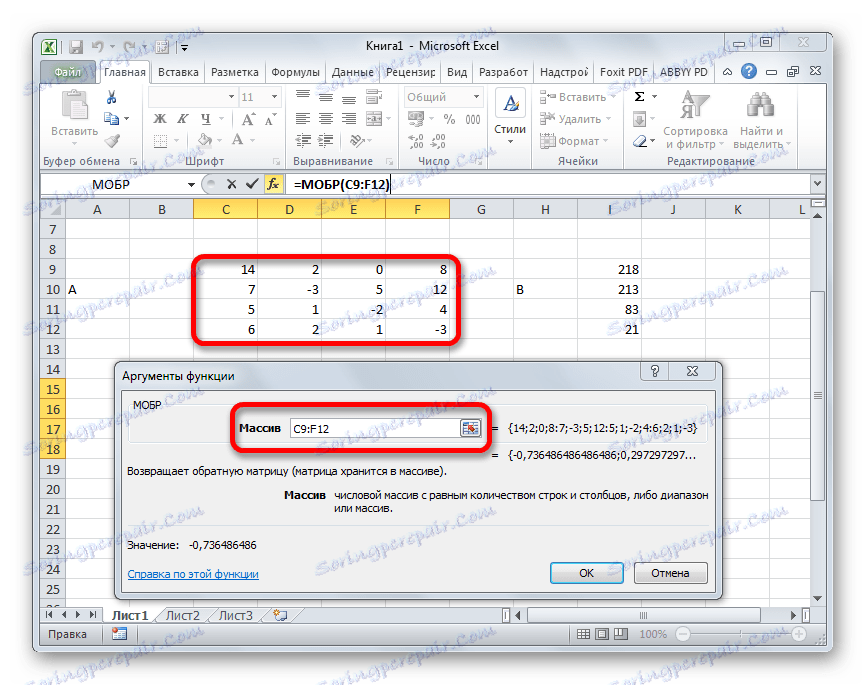
5. Отваря се прозорецът на аргументите на функцията MOBR. Има само едно поле в броя аргументи - "Array" . Тук трябва да посочите адреса на нашата таблица. За тази цел зададохме курсора в това поле. След това задръжте левия бутон на мишката и изберете областта на листа, където се намира матрицата. Както можете да видите, данните за координатите на местоположенията се въвеждат автоматично в полето на прозореца. След като тази задача е завършена, най-очевидно би било да кликнете върху бутона "OK" , но не бързайте. Факт е, че кликването върху този бутон е еквивалентно на използването на командата Enter . Но когато работите с масиви след като завършите въвеждането на формулата, не трябва да кликвате върху бутона Enter , но да направите набор от клавишни комбинации Ctrl + Shift + Enter . Извършваме тази операция.
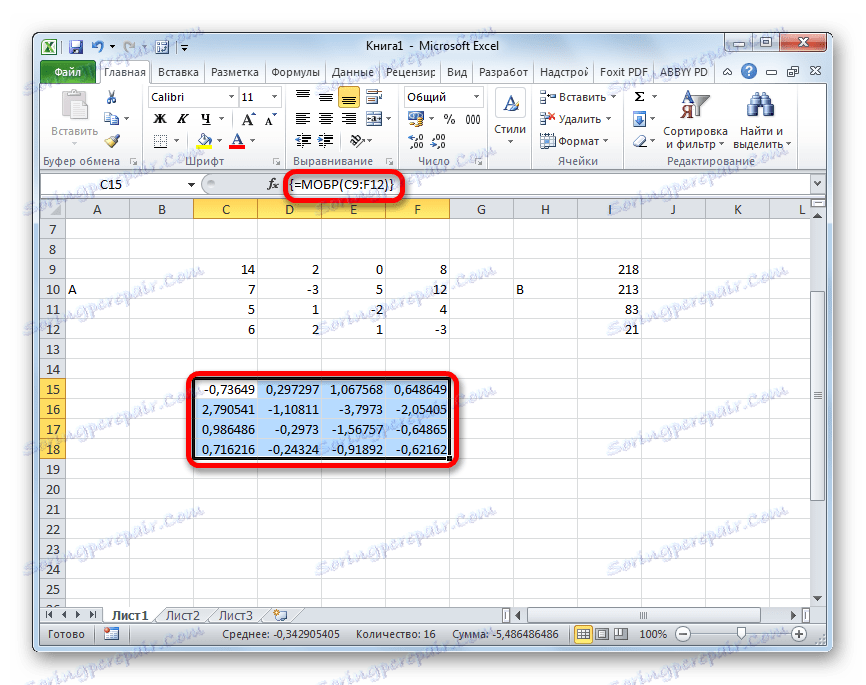
6. След това програмата изпълнява изчисления и на изхода в предварително разпределената област имаме матрица, обратно на това.
7. Сега трябва да умножим обратната матрица от матрицата В , която се състои от една колона от стойности, разположени след равен знак в изразите. За умножение на таблици в Excel има и отделна функция, която се нарича ЧОВЕК . Това изявление има следния синтаксис:

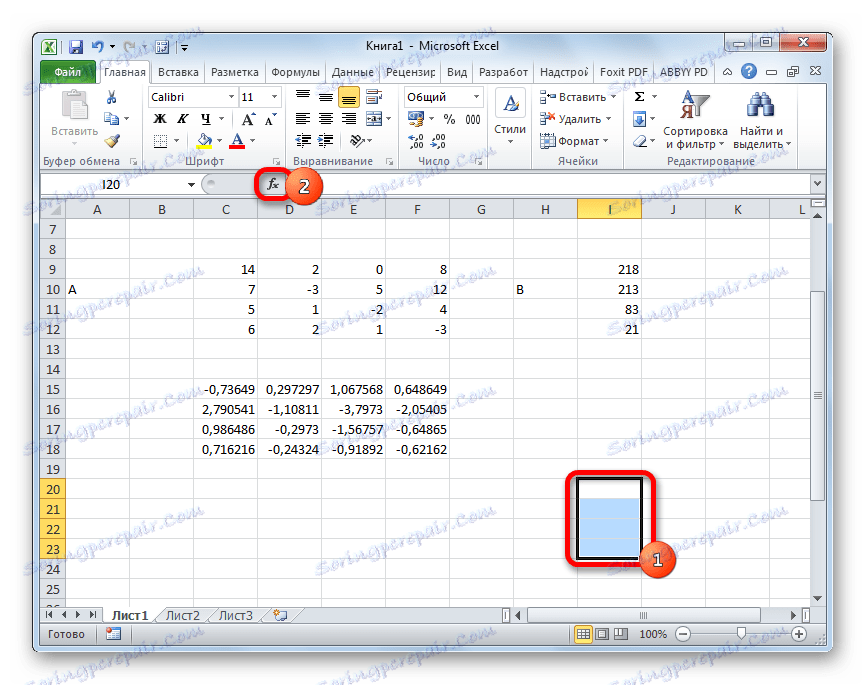
   =МУМНОЖ(Массив1;Массив2)

   Избираме диапазона, в нашия случай, състоящ се от четири клетки. След това отново стартирайте Помощника за функции, като кликнете върху иконата "Вмъкване на функция" .

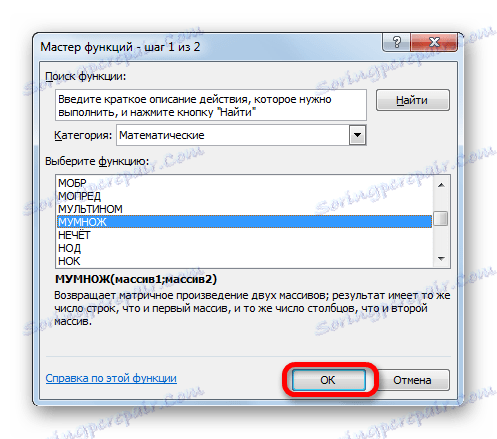
8. В категорията "Математически" , в началото на Wizard на функциите , изберете името "HUMBLE" и кликнете върху бутона "OK" .
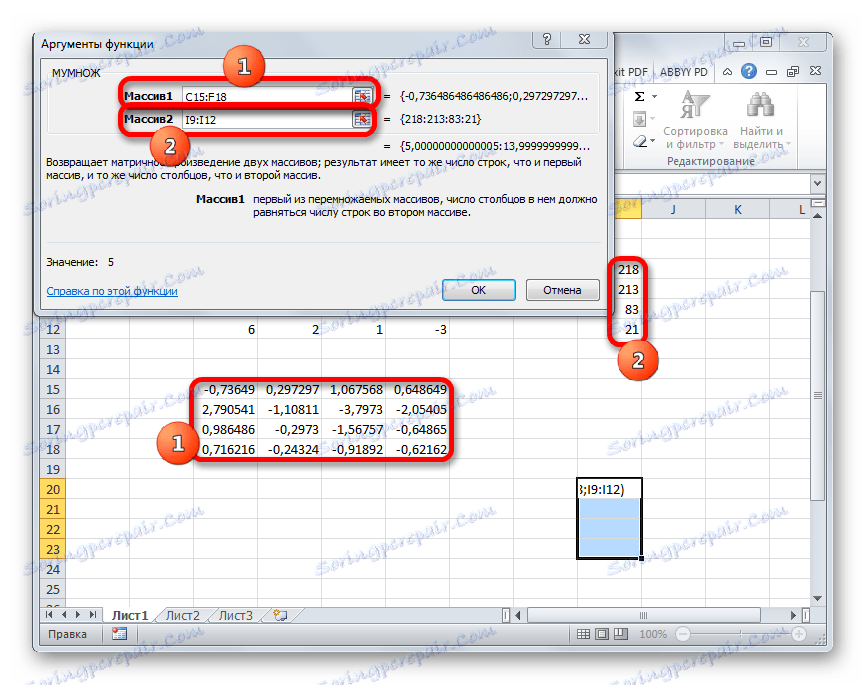
9. Прозорецът на аргументите на функцията MULTI . В полето "Array1" въвеждаме координатите на нашата обратна матрица. За това, както и в последния момент, настроихме курсора в полето и с натиснат левия бутон на мишката, изберете съответната таблица с курсора. Извършваме подобно действие за въвеждане на координати в полето "Array2" , само този път избираме стойностите в колона Б. След като изпълните горните действия, отново не бързайте да натискате бутона "OK" или клавиша Enter и въведете Ctrl + Shift + Enter .
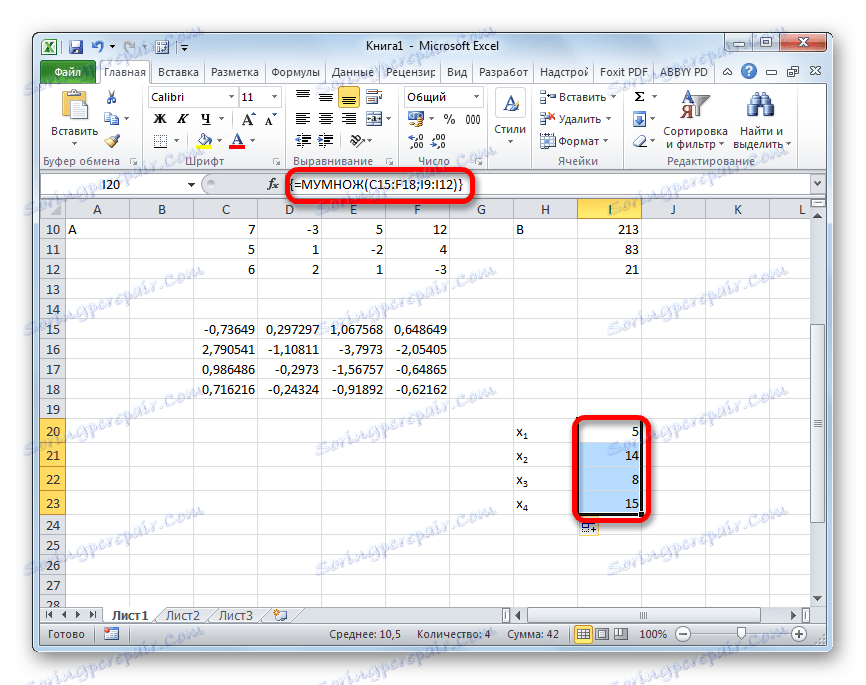
10. След това действие корените на уравнението се показват в предварително избраната клетка: X1 , X2 , X3 и X4 . Те ще бъдат подредени последователно. По този начин можем да кажем, че решихме тази система. За да се провери правилността на решението, е достатъчно да се заместят тези корени за оригиналната система на изрази. Ако се наблюдава равенство, това означава, че представената система от уравнения се решава правилно.

Урокът: Обратната матрица в Excel

Метод 2: избор на параметри

Вторият известен метод за решаване на системата от уравнения в Excel е прилагането на метода за избор на параметри. Същността на този метод се крие в търсенето на обратното. Тоест, въз основа на известен резултат, търсим неизвестен аргумент. Да използваме квадратичното уравнение

3x^2+4x-132=0

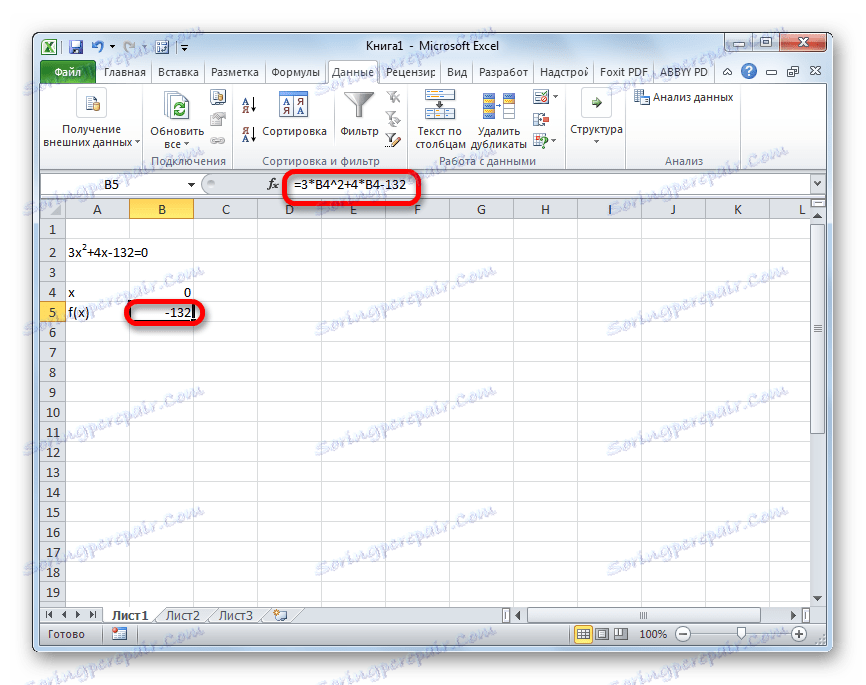
1. Да приемем стойността на x за равен 0 . Изчисляваме съответната стойност f (x), като прилагаме следната формула:

   =3*x^2+4*x-132

   Вместо стойността на "X" заместете адреса на клетката, където се намира числото 0 , което взехме за x .

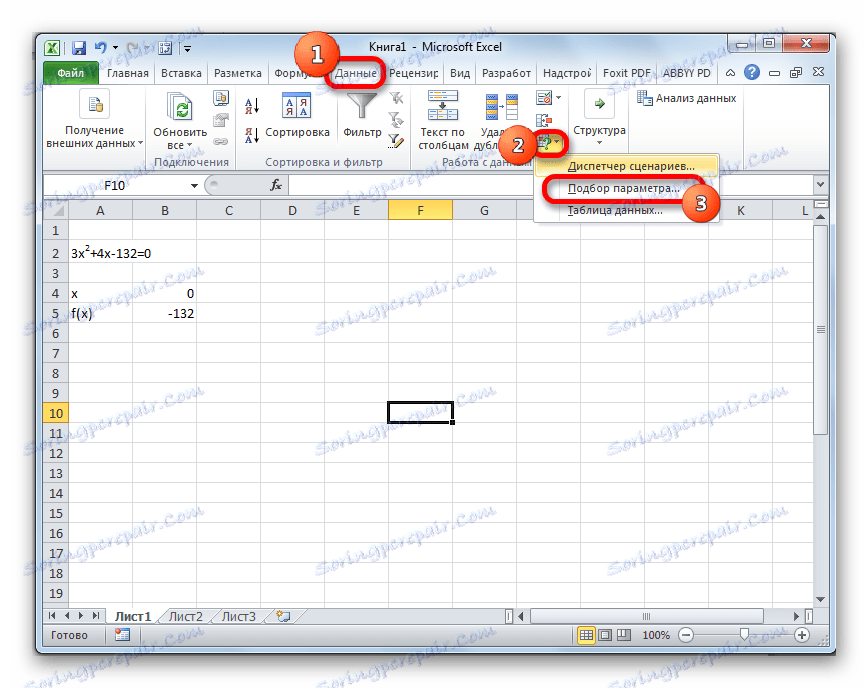
2. Отворете раздела "Данни" . Кликнете върху бутона "Анализ на какво, ако" . Този бутон се намира на лентата в полето "Работа с данни" . Появява се падащ списък. Изберете елемента " Избор на параметри ..." в него .
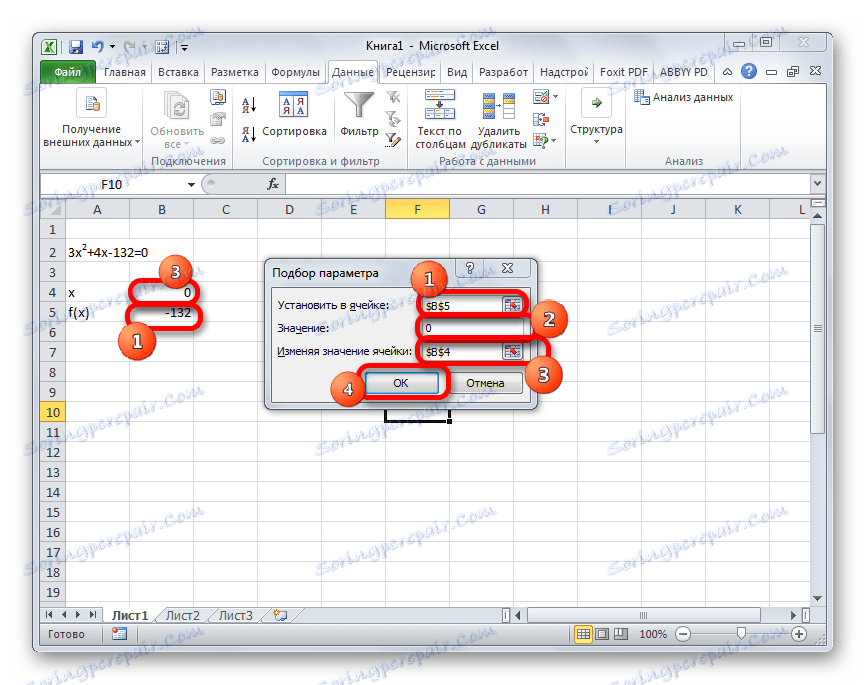
3. Прозорецът за избор на параметри започва. Както можете да видите, той се състои от три полета. В полето "Задайте в клетката" посочваме адреса на клетката, в която се намира формулата f (x) , изчислена от нас малко по-рано. В полето "Стойност" въведете числото "0" . В полето "Промяна на стойностите" посочваме адреса на клетката, в която се намира стойността на x , която преди това е взета от нас за 0 . След като изпълните тези стъпки, кликнете върху бутона "OK" .
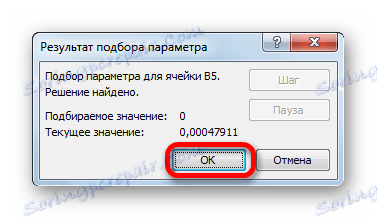
4. След това Excel ще извърши изчислението, като избере параметъра. Това ще бъде съобщено от информационния прозорец, който се появи. В него кликнете върху бутона "OK" .
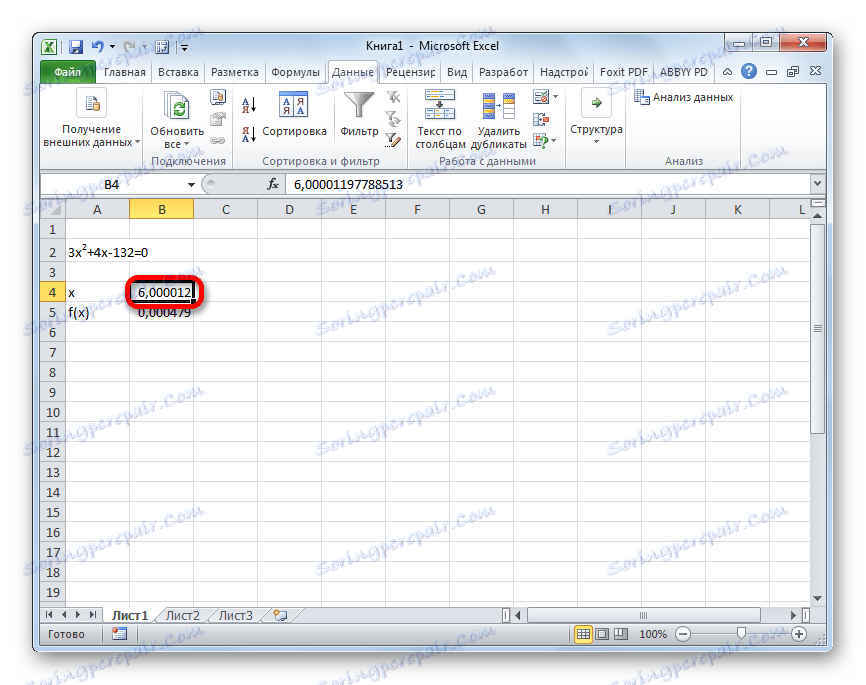
5. Резултатът от изчисляването на корена на уравнението ще бъде в клетката, която сме задали в полето "Промяна на стойностите" . В нашия случай, както виждаме, х ще бъде равен на 6 .

Този резултат може да бъде проверен и чрез заместване на тази стойност в решаващия израз, вместо на стойността x .

Урокът: Избор на параметри в Excel

Метод 3: Метод на Креймър

Сега нека се опитаме да решим системата от уравнения по метода Cramer. Например вземете същата система, която е била използвана в режим 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


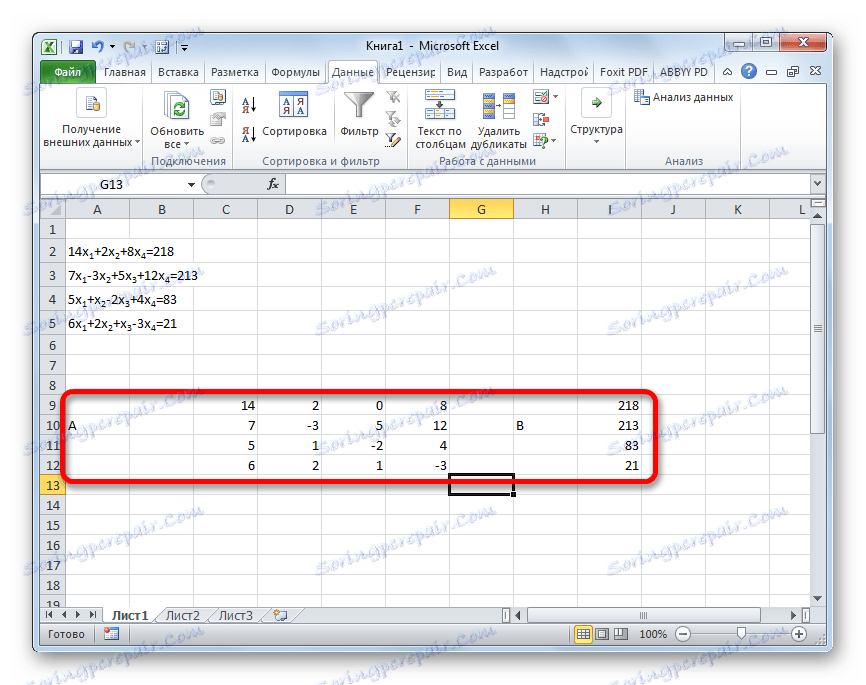
1. Както в първия метод, съставяме матрицата А от коефициентите на уравненията и таблицата Б от стойностите, които стоят след знака "равен" .
2. Тогава правим още четири маси. Всеки от тях е копие на матрица А , само за тези копия една колона се заменя с таблица Б алтернативно. Първата таблица има първата колона, втората има втората колона и т.н.
3. Сега трябва да изчислим детерминантите за всички тези таблици. Системата от уравнения ще има решения само ако всички детерминанти имат стойност, различна от нула. За да изчислите отново тази стойност в Excel, има отделна функция - MOPRED . Синтаксисът на този оператор е:

   =МОПРЕД(массив)

   По този начин, както в случая на функцията MBD , единственият аргумент е препратка към обработваната таблица.

   Така че, изберете клетката, в която ще се показва детерминанта на първата матрица. След това кликнете върху бутона "Вмъкни функция" , който е познат от предишните методи.

4. Прозорецът Магьосници е активиран. Преминаваме в категорията "Математически" и сред списъка с оператори избираме името "MOPRED" там . След това кликнете върху бутона "OK" .
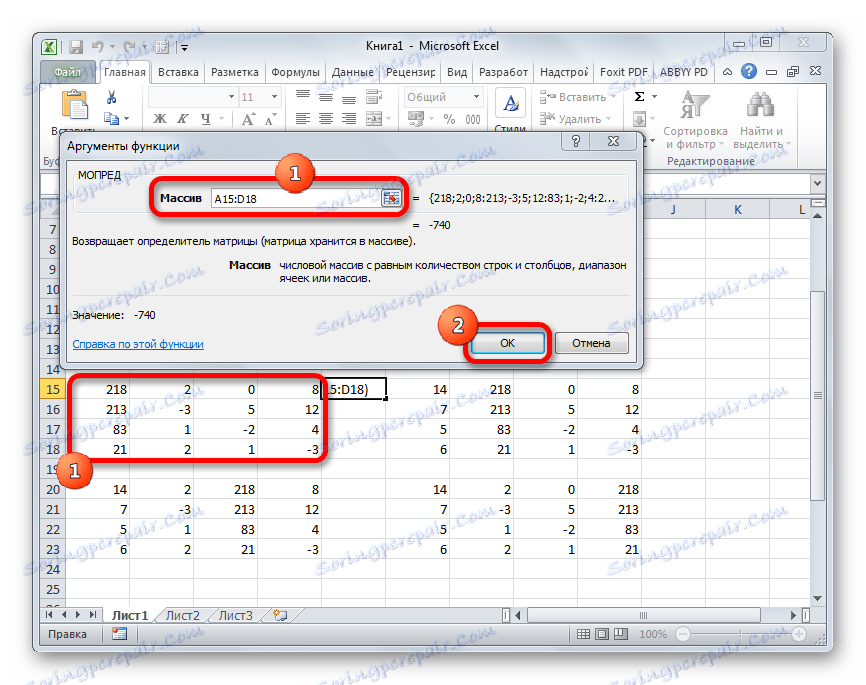
5. Отваря се прозореца на аргументите на функцията MOPED . Както виждате, има само едно поле - "Array" . В това поле въвеждаме адреса на първата трансформирана матрица. За да направите това, задайте курсора в полето и след това изберете обхвата на матрицата. След това кликнете върху бутона "OK" . Тази функция извежда резултата в една клетка, а не в масив, така че не е необходимо да натискате Ctrl + Shift + Enter, за да получите изчислението.
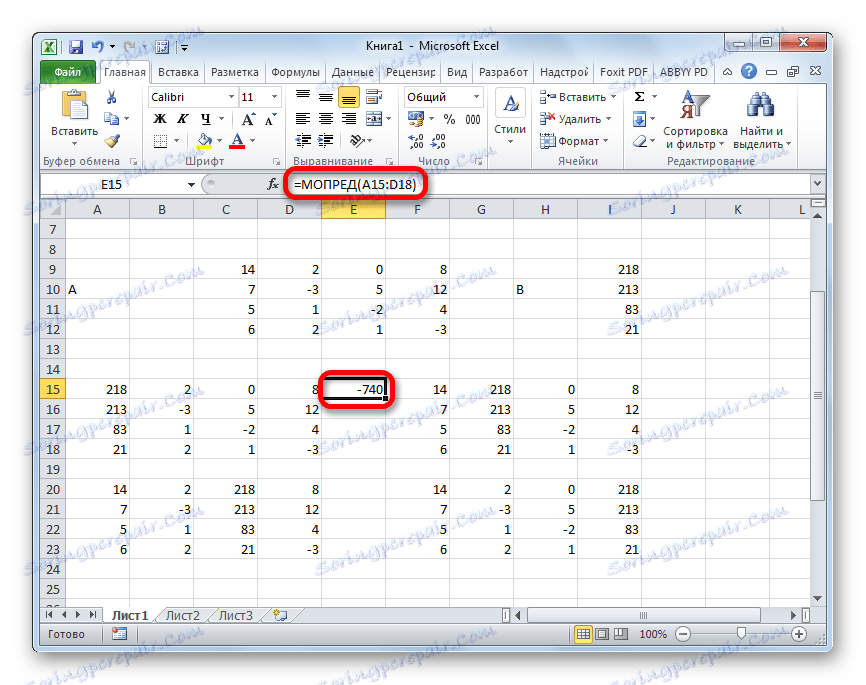
6. Функцията изчислява резултата и го извежда в предварително избрана клетка. Както виждате, в нашия случай детерминантът е -740 , т.е. той не е равен на нула, което е подходящо за нас.
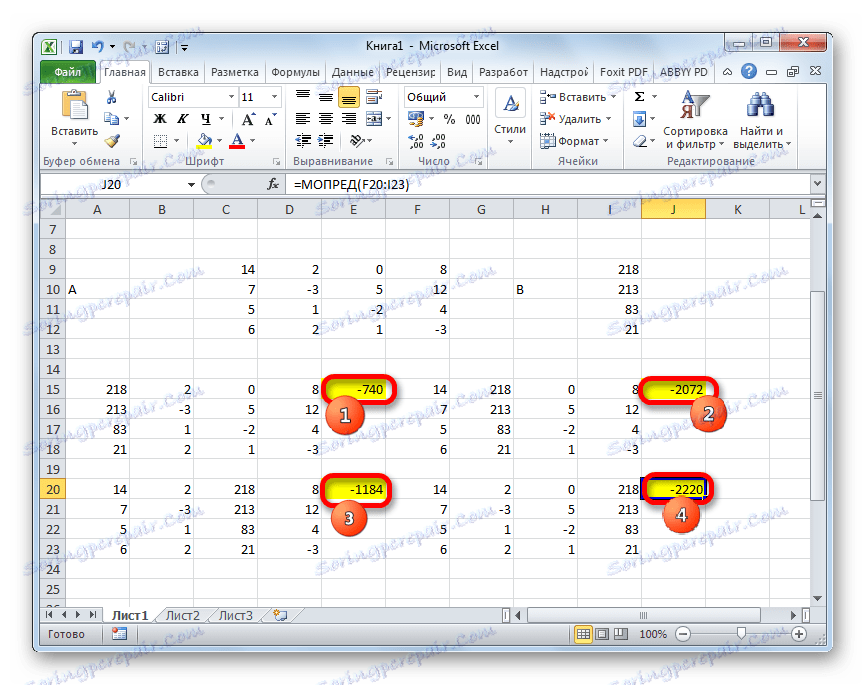
7. По подобен начин изчисляваме детерминантите за останалите три таблици.
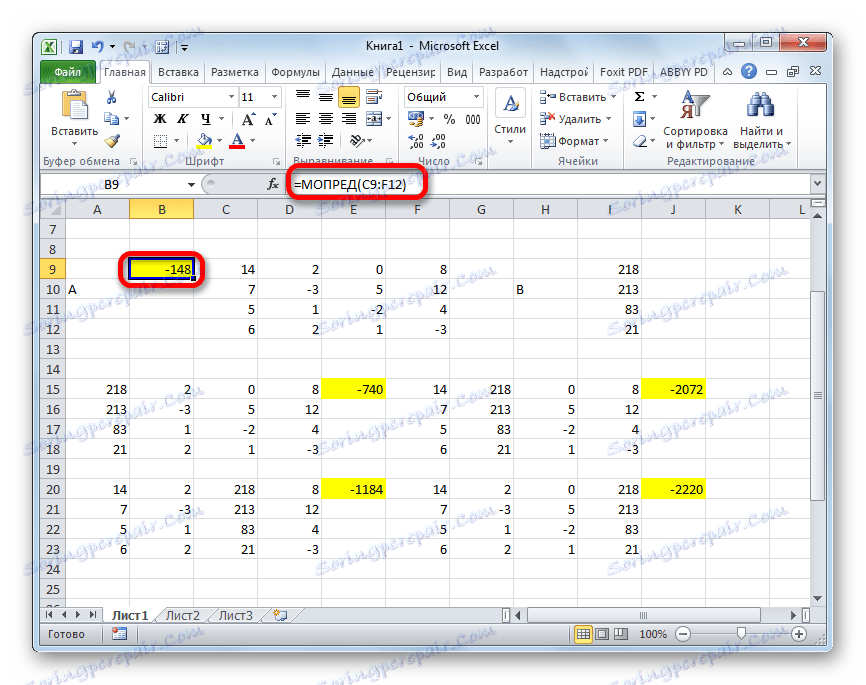
8. В последния етап изчисляваме детерминанта на първичната матрица. Процедурата е една и съща за същия алгоритъм. Както можете да видите, детерминанта на първичната таблица също е различен от нула и оттам матрицата се счита за недегенна, т.е. системата от уравнения има решения.
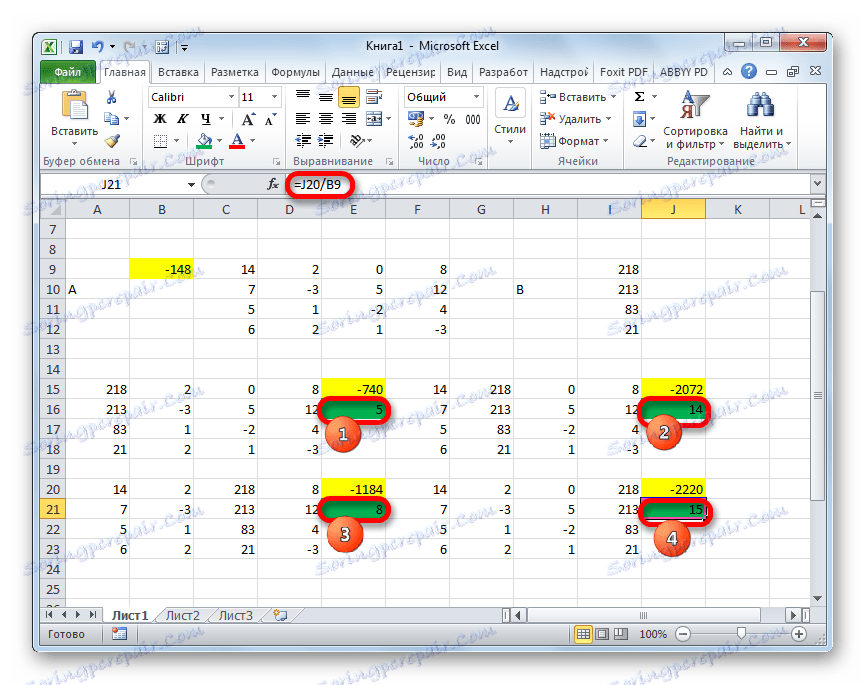
9. Сега е време да намерим корените на уравнението. Коренът на уравнението ще бъде равен на съотношението на детерминанта на съответната трансформирана матрица към детерминанта на първичната таблица. Следователно, след разделянето на четирите детерминанта на трансформираните матрици един по един -148 , който е определящ за оригиналната таблица, получаваме четири корена. Както можете да видите, те са равни на стойностите 5 , 14 , 8 и 15 . По този начин те съвпадат точно с корените, които открихме, използвайки обратната матрица в метод 1 , което потвърждава коректността на решението на системата от уравнения.

Метод 4: Gauss методът

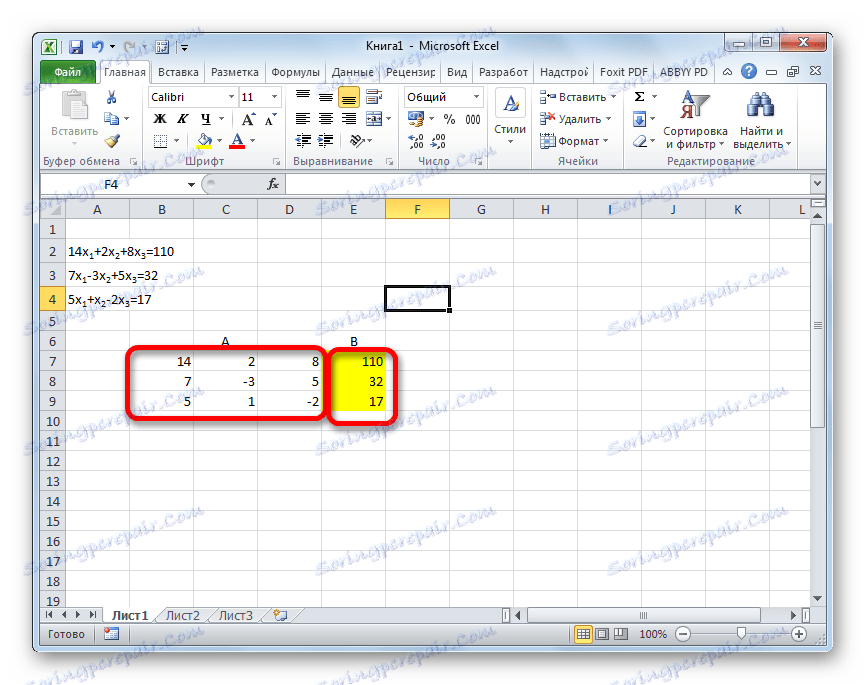
Решаването на системата от уравнения може да се направи и с помощта на Gauss метод. Например, нека вземем по-проста система от уравнения от три неизвестни:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


1. Отново записваме последователно коефициентите в таблица А и свободните термини, които се намират след знака "се равнява" на таблица Б. Но този път ще доближим двете маси, тъй като това ще е необходимо, за да можем да работим в бъдеще. Важно условие е, че в първата клетка на матрицата А стойността е различна от нула. В противен случай трябва да пренаредите редовете на места.
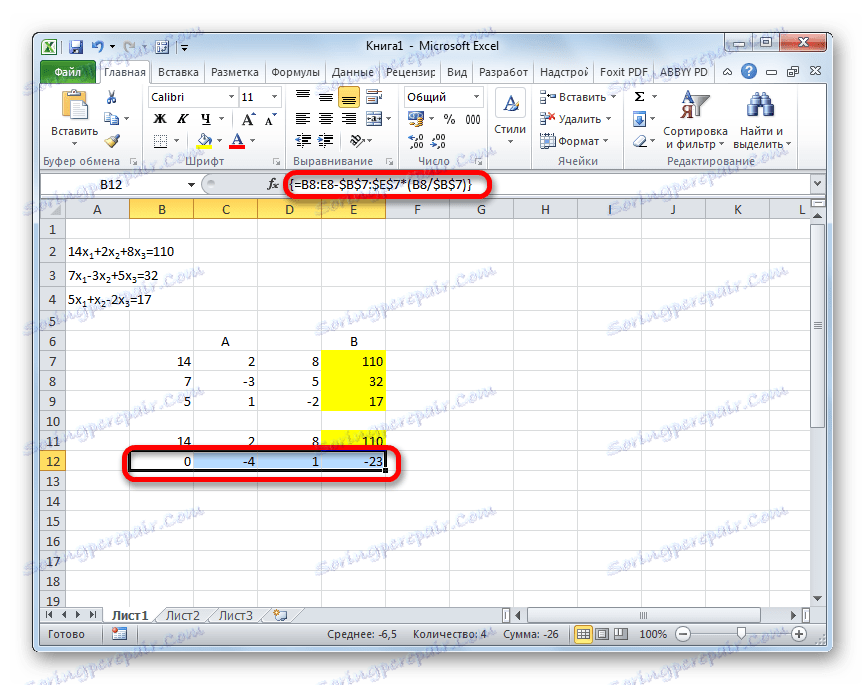
2. Копирайте първия ред от две свързани матрици в ред по-долу (за яснота можете да пропуснете един ред). В първата клетка, която се намира в реда дори по-ниска от предишната, въведете следната формула:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Ако подредите матриците по различен начин, адресите на клетките с формулата ще имат различна стойност за вас, но можете да ги изчислите, като ги сравнявате с формулите и изображенията, които са дадени тук.

   След като въведете формулата, изберете целия ред клетки и натиснете Ctrl + Shift + Enter . Формулата на масива ще бъде приложена към реда и ще бъде попълнена със стойности. По този начин извадихме от втория ред първия, умножен по съотношението на първите коефициенти на първите два израза на системата.

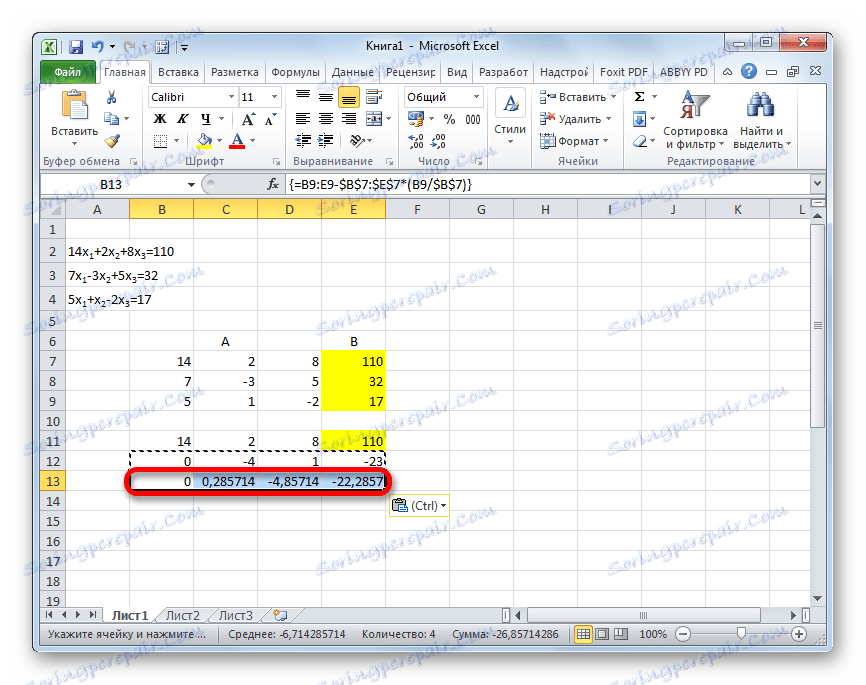
3. След това копирайте последващата линия и я поставете в реда по-долу.
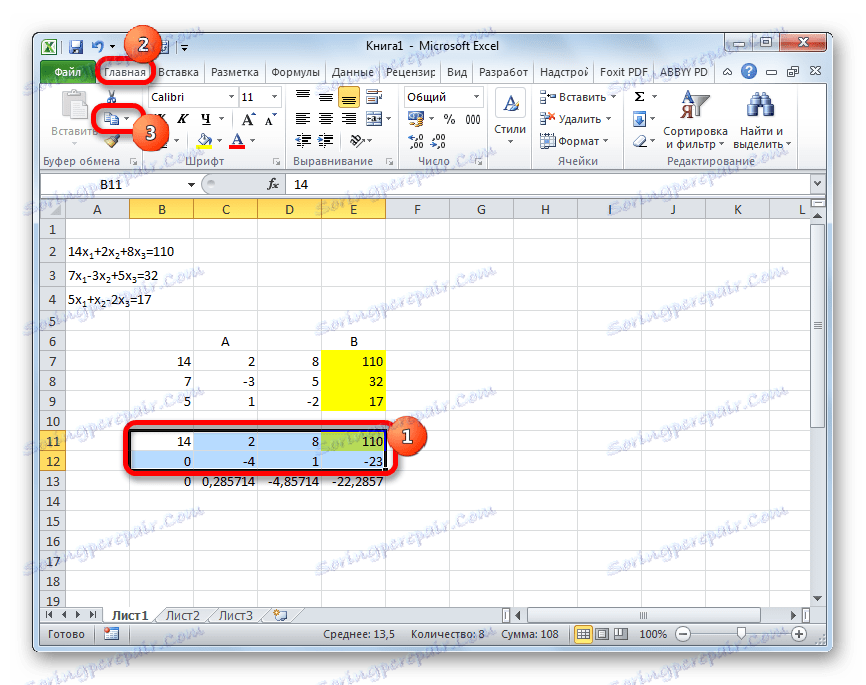
4. Изберете първите два реда след липсващата линия. Кликнете върху бутона "Копиране" , който се намира на лентата в раздела "Начало" .
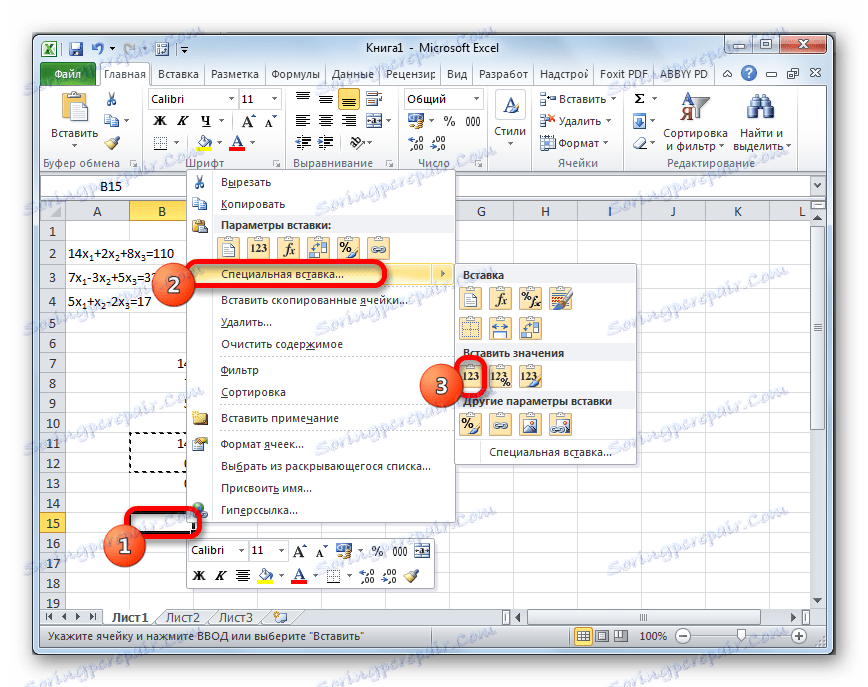
5. Прескачаме линията след последния запис на листа. Изберете първата клетка в следващия ред. Щракнете с десния бутон на мишката. В отвореното контекстно меню задържаме курсора върху елемента "Специална паста" . В допълнителния списък, който започва, изберете елемента "Стойности" .
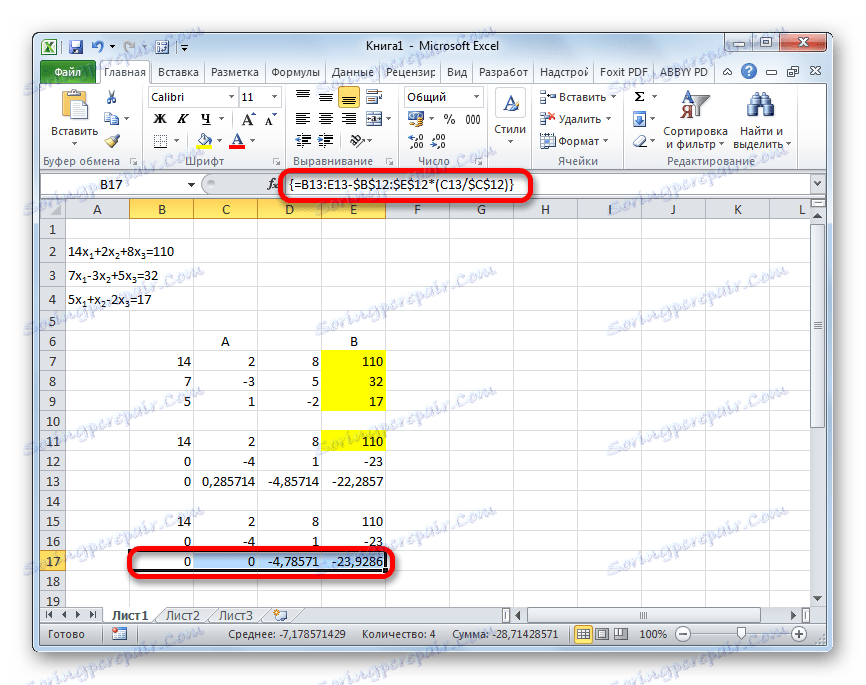
6. В следващия ред въведете формулата на масива. Той изважда втория ред от третия ред на предишната група данни, умножен по съотношението на втория коефициент на третия и втория ред. В нашия случай формулата ще има следната форма:

   =B13:E13-$B$12:$E$12*(C13/$C$12)

   След като въведете формулата, изберете цялата серия и приложете клавишната комбинация Ctrl + Shift + Enter .

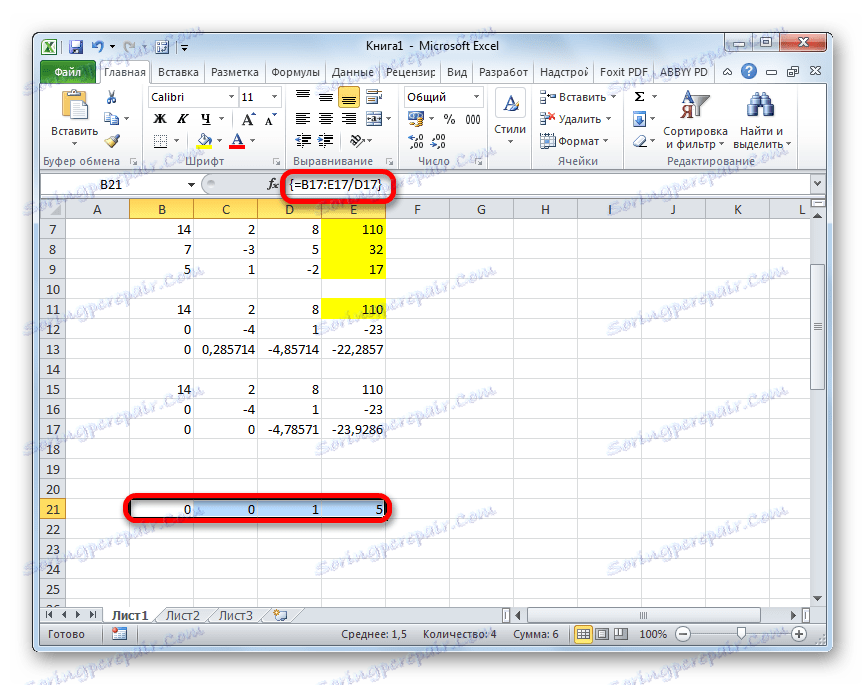
7. Сега е необходимо да се извърши обратна работа, като се използва Gauss методът. Пропускаме три реда от последния запис. На четвъртия ред въвеждаме формулата на масива:

   =B17:E17/D17

   По този начин разделяме последната линия, която изчислихме по третия си коефициент. След като въведете формулата, изберете целия ред и натиснете Ctrl + Shift + Enter .

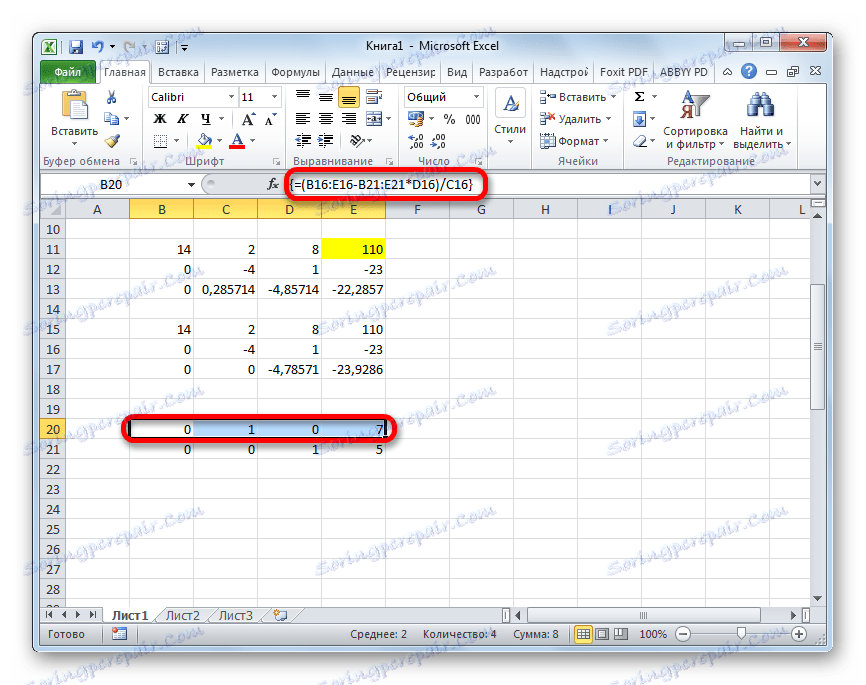
8. Ние се издигаме на линията нагоре и влизаме в нея със следната формула на масива:

   =(B16:E16-B21:E21*D16)/C16

   Натискаме обичайната комбинация от клавиши, за да приложим формулата на масива.

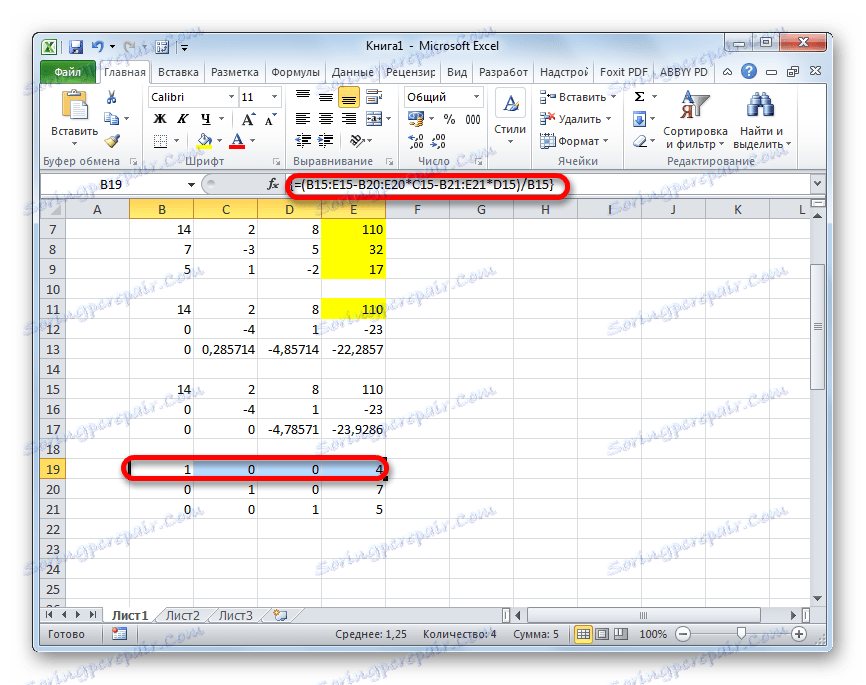
9. Повишаваме се още една линия. В нея въвеждаме формулата на масива от следната форма:

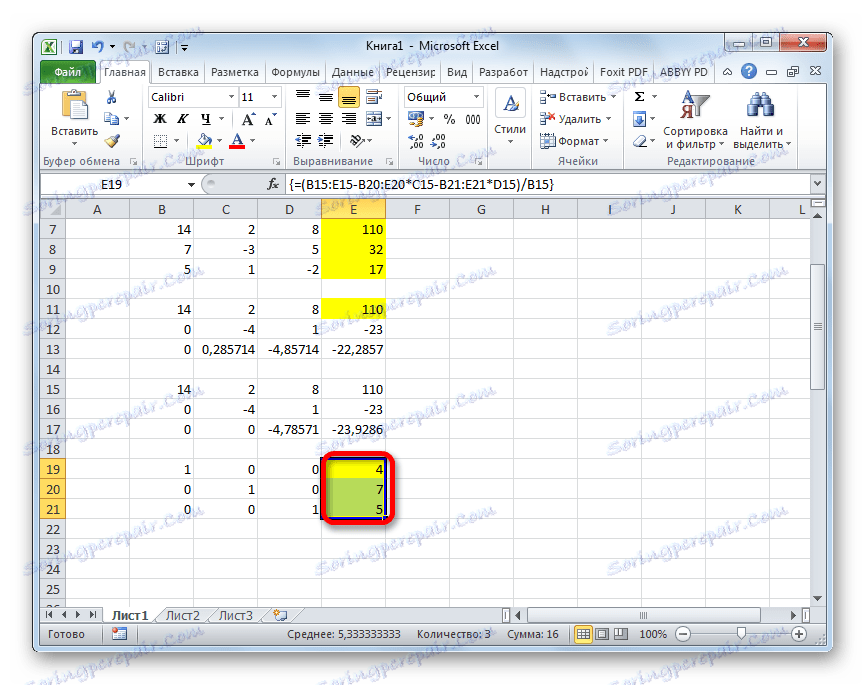
   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Отново изберете целия ред и приложете комбинацията от клавиши Ctrl + Shift + Enter .

10. Сега разгледайте номерата, получени в последната колона на последния блок от линии, изчислени от нас по-рано. Тези числа ( 4 , 7 и 5 ) ще бъдат корените на дадена система от уравнения. Можете да проверите това, като замените тях вместо X1 , X2 и X3 в изразите.

Както можете да видите, в Excel системата на уравненията може да бъде решена чрез редица методи, всяка от които има своите предимства и недостатъци. Но всички тези методи могат условно да бъдат разделени на две големи групи: матрица и използване на инструмента за избор на параметри. В някои случаи не винаги матричните методи са подходящи за решаване на проблема. По-специално, когато детерминанта на матрицата е нула. В други случаи потребителят е свободен да реши кой вариант смята за по-удобен за себе си.

• ← Изграждане на парабола в Microsoft Excel
• Създаване на бутон в Microsoft Excel →