Excel

Изчисляване на функцията Laplace в Microsoft Excel

Една от най-известните неелементарни функции, използвани в математиката, в теорията на диференциалните уравнения, в статистиката и в теорията на вероятностите е функцията Лаплас. Решаването на проблеми с него изисква значителна подготовка. Нека да разберете как можете да изчислите този показател с помощта на инструменти на Excel.

Функцията Лаплас

Функцията Лаплас има широко практическо и теоретично приложение. Например, често се използва за решаване на диференциални уравнения. Този термин има още едно еквивалентно име - вероятността интеграл. В някои случаи основата за решението е изграждането на таблица със стойности.

Оператор NORM.ST.DIST

В Excel този проблем се решава с помощта на оператора NORM.ST. RASP . Неговото име е съкращение от термина "нормално стандартно разпространение". Тъй като основната й задача е да се върне към разпределената клетка стандартно нормално интегрално разпределение. Този оператор принадлежи към статистическата категория на стандартните функции на Excel.

В Excel 2007 и в по-ранните версии на програмата този оператор се нарича NORMSDIST . Също така се поддържа в съвместимост със съвременните версии на приложенията. Но все пак те препоръчват използването на по-напреднал аналог - NORMST.RASP .

Синтаксисът на оператора NORM.ST RASP е както следва:

=НОРМ.СТ.РАСП(z;интегральная)

Остарелия оператор NORMSDIST е написан, както следва:

=НОРМСТРАСП(z)

Както можете да видите, в новия вариант аргументът "Интеграл" е добавен към съществуващия аргумент "Z " . Трябва да се отбележи, че всеки аргумент е задължителен.

Аргументът "Z" показва числената стойност, за която е конструирано разпределението.

Аргументът "Integral" е логическа стойност, която може да има "TRUE" ("1") или "FALSE" ("0") . В първия случай функцията за интегрална дистрибуция се връща в посочената клетка, а във втория - функцията за разпределение на теглото.

Решаване на проблема

За да се извърши необходимото изчисление за дадена променлива, се прилага следната формула:

=НОРМ.СТ.РАСП(z;интегральная(1))-0,5

Сега нека използваме конкретен пример, за да разгледаме използването на оператора NORM.ST RASP за решаване на конкретен проблем.

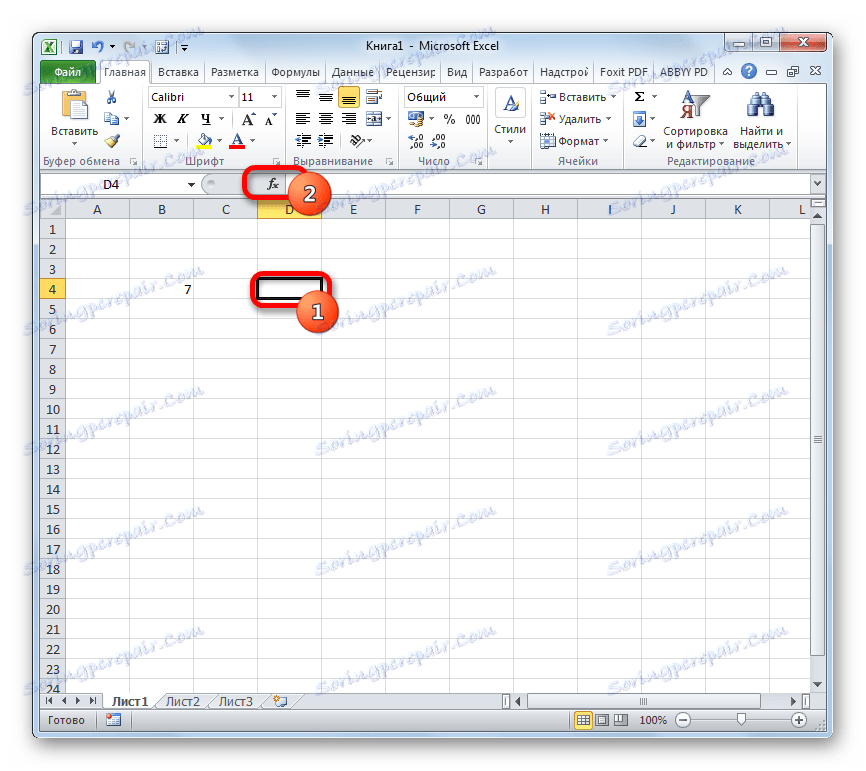
  1. Изберете клетката, където ще се покаже готовият резултат, и кликнете върху иконата "Insert function" , разположена близо до линията на формулата.

    2. Отидете в съветника за функции в Microsoft Excel

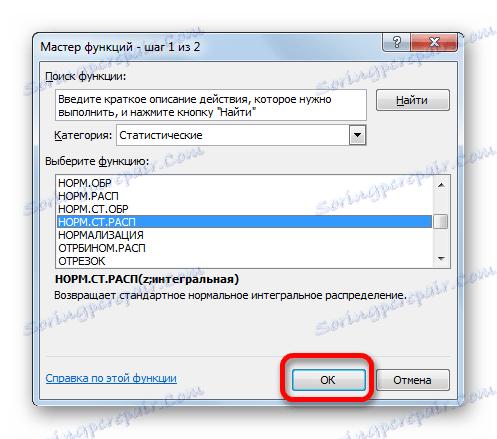
  2. След отварянето на функциите на съветника отидете в категорията "Статистически" или "Пълен азбучен списък" . Изберете името "NORM.ST.RASP" и кликнете върху бутона "OK" .

    3. Отворете прозореца за аргументи на функцията NORM.STDIST в Microsoft Excel

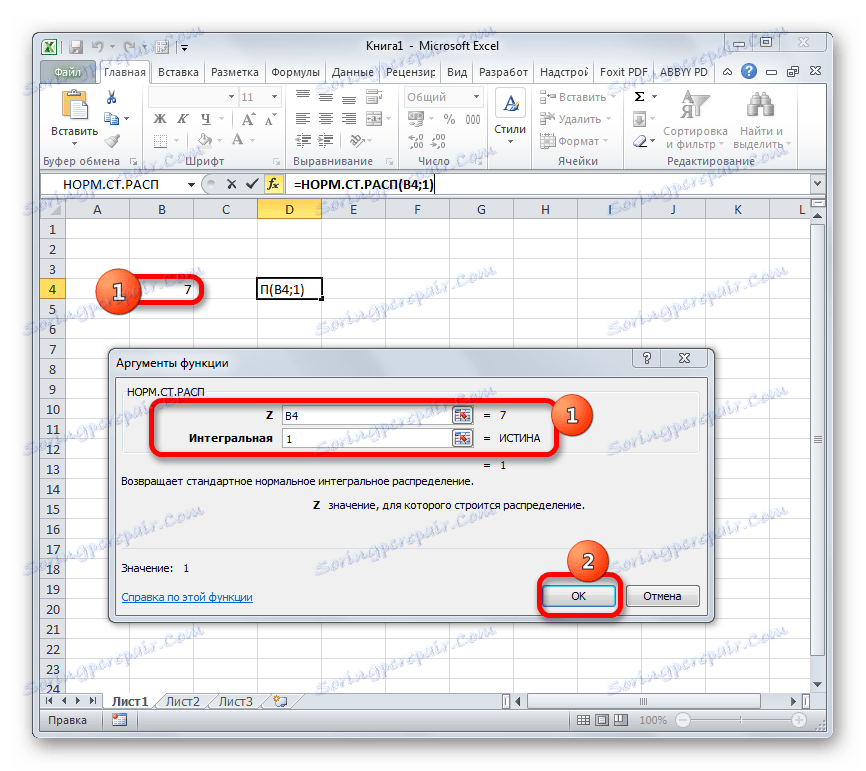
  3. Прозорецът на аргументите на оператора NORM.ST.RESP е активиран . В полето "Z" въведете променливата, която искате да изчислите. Също така, този аргумент може да бъде представен като препратка към клетката, която съдържа тази променлива. В полето "Интегрално " въведете стойността "1" . Това означава, че операторът връща функцията за интегрално разпределение като решение след изчислението. След като изпълните горните стъпки, кликнете върху бутона "OK" .

    4. Прозорецът с аргументи на функцията NORM.STDIST в Microsoft Excel

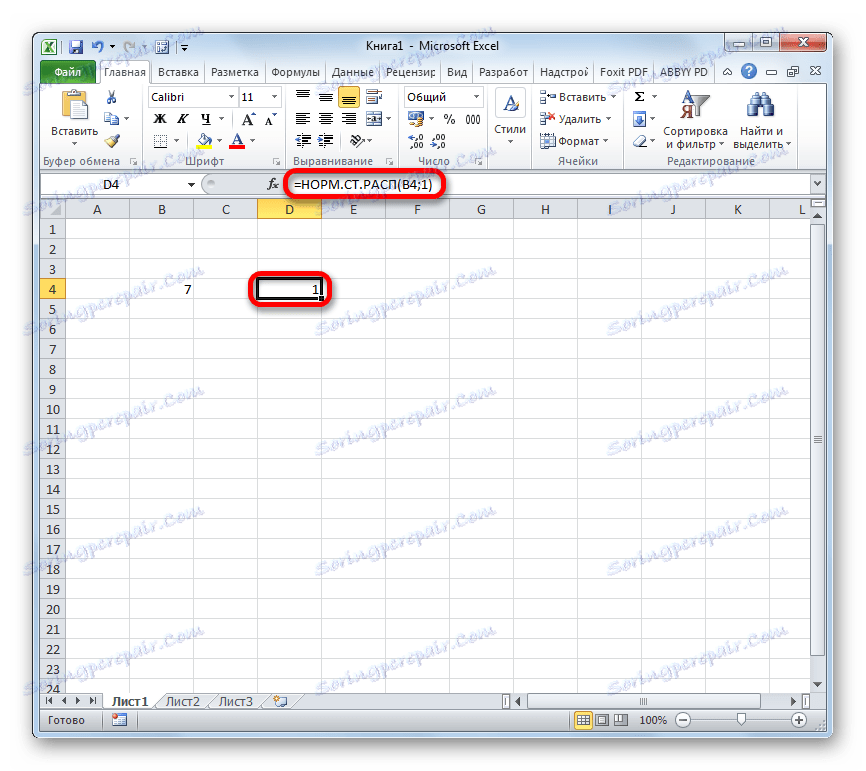
  4. След това резултатът от обработката на данните от оператора NORM.ST.DIST ще бъде показан в клетката, която е посочена в първия параграф на това ръководство.

    5. Резултатът от изчисляването на функцията NORM.STDIST в Microsoft Excel

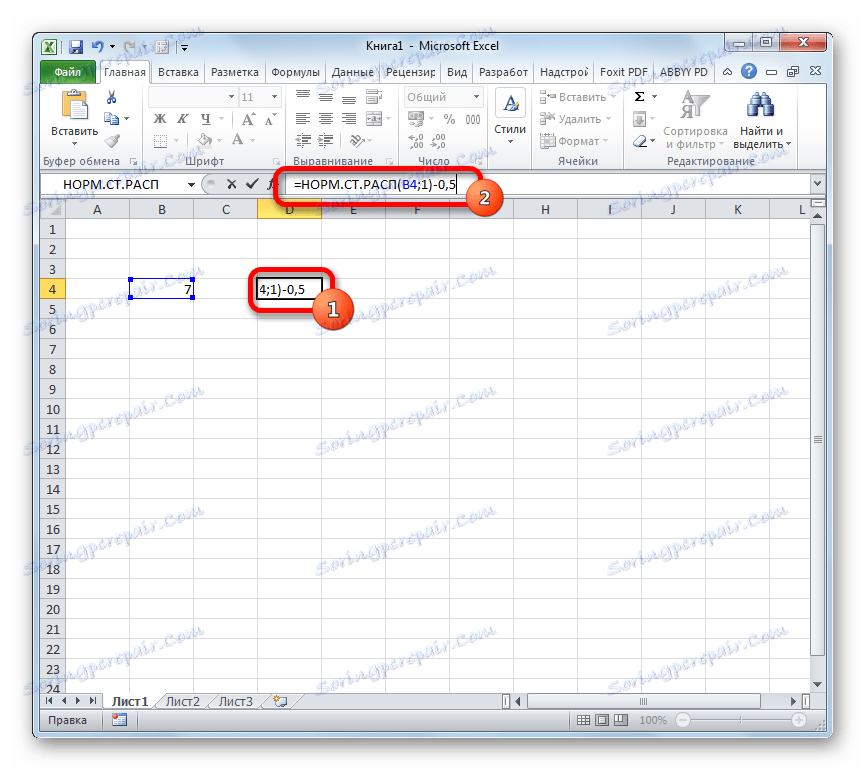
  5. Но това не е всичко. Изчислихме само стандартното нормално интегрално разпределение. За да се изчисли стойността на функцията Laplace, трябва да се вземе числото 0.5 извън нея. Изберете клетката, съдържаща израза. В реда на формулата, след израза NORM.ST RASP, добавете стойността: -0.5 .

    6. Формулата за изчисляване на функцията Laplace в Microsoft Excel

  6. За да извършите изчислението, натиснете бутона Enter . Резултатът е желаната стойност.

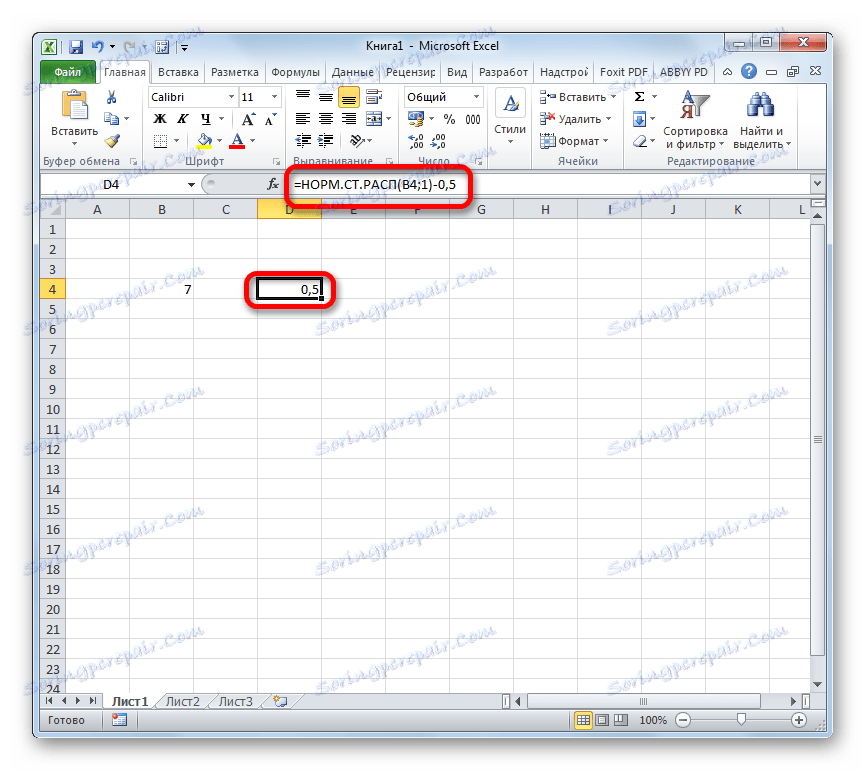
Резултатът от изчисляването на функцията Laplace в Microsoft Excel

Както можете да видите, не е трудно да се изчисли функцията Laplace за конкретна дадена цифрова стойност в Excel. За тези цели се използва стандартният оператор NORM.ST.RESP .