Изчисляване на доверителния интервал в Microsoft Excel
Един от методите за решаване на статистически проблеми е изчисляването на доверителния интервал. Той се използва като по-предпочитана алтернатива на точковата оценка с малък размер на извадката. Трябва да се отбележи, че процесът на изчисляване на самия доверителен интервал е доста сложен. Но инструментите на програмата Excel ни позволяват да я опростим донякъде. Нека да разберем как това се прави на практика.
Прочетете още: Статистически функции в Excel
съдържание
Процедура на изчисление
Този метод се използва за интервал за оценка на различни статистически променливи. Основната задача на това изчисление е да се отървем от неопределеността на точковата оценка.
В Excel има две основни опции за извършване на изчисления, като се използва този метод: когато разликата е известна и когато не е известна. В първия случай функцията BELIEVE.NORM се използва за изчисления, а във втория - TRUST .
Метод 1: Функцията TRUST NORM
Операторът BELIEVE.NORM , свързан със статистическата група от функции, за пръв път се появи в Excel 2010. В по-ранните версии на тази програма се смята , че аналогът е. Задачата на този оператор е да изчисли доверителен интервал с нормално разпределение за средната популация.
Синтаксисът му е както следва:
=ДОВЕРИТ.НОРМ(альфа;стандартное_откл;размер)
"Алфа" е аргумент, който показва нивото на значимост, което се използва за изчисляване на нивото на доверие. Ниво на доверие е равно на следния израз:
(1-«Альфа»)*100
"Стандартното отклонение" е аргумент, чиято същност е ясно от името. Това е стандартното отклонение на предложената извадка.
"Размер" е аргументът, който определя размера на извадката.
Всички аргументи на този оператор са задължителни.
Функцията TRUST има точно същите аргументи и възможности като предишната. Синтаксисът му е следният:
=ДОВЕРИТ(альфа;стандартное_откл;размер)
Както можете да видите, разликите са само в името на оператора. Посочената функция остава за целите на съвместимостта в Excel 2010 и в по-нови версии в специалната категория "Съвместимост" . Във версиите на Excel 2007 и по-рано, той присъства в главната група статистически оператори.
Доверителният интервал се определя, като се използва следната формула:
X+(-)ДОВЕРИТ.НОРМ
Където X е средната стойност на пробата, която се намира в средата на избрания диапазон.
Сега нека разгледаме как да изчислим интервала на доверието за конкретен пример. Бяха проведени дванадесет теста, в резултат на които в таблицата бяха отразени различни резултати. Това е нашето общо. Стандартното отклонение е 8. Трябва да изчислим доверителния интервал с ниво на доверителност 97%.
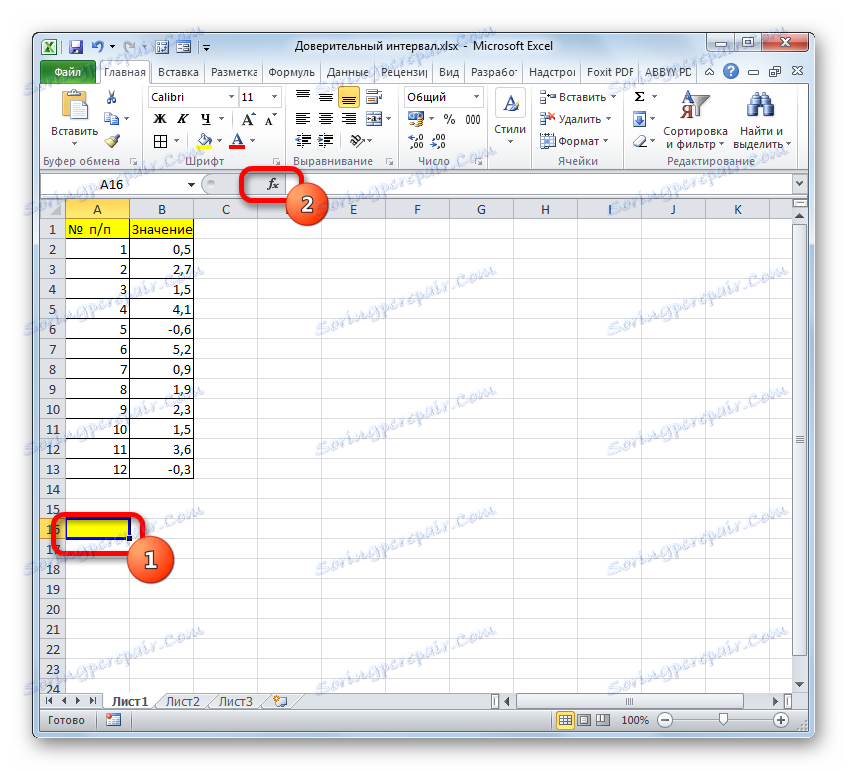
- Изберете клетката, където ще се покаже резултатът от обработката на данните. Кликваме върху бутона "Вмъкване на функция" .
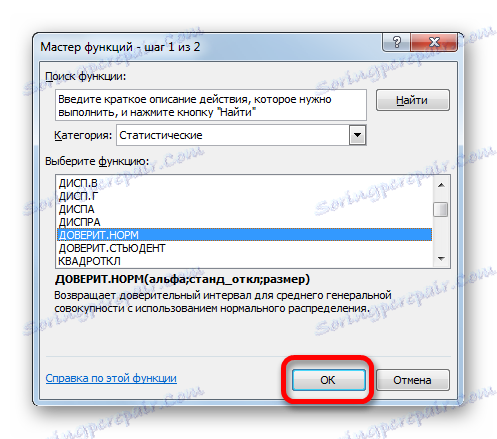
- Появява се съветникът за функциите . Отворете категорията "Статистически" и изберете името "Доверие" . След това кликнете върху бутона "OK" .
- Отваря прозорец с аргументи. Полетата му естествено съответстват на имената на аргументите.
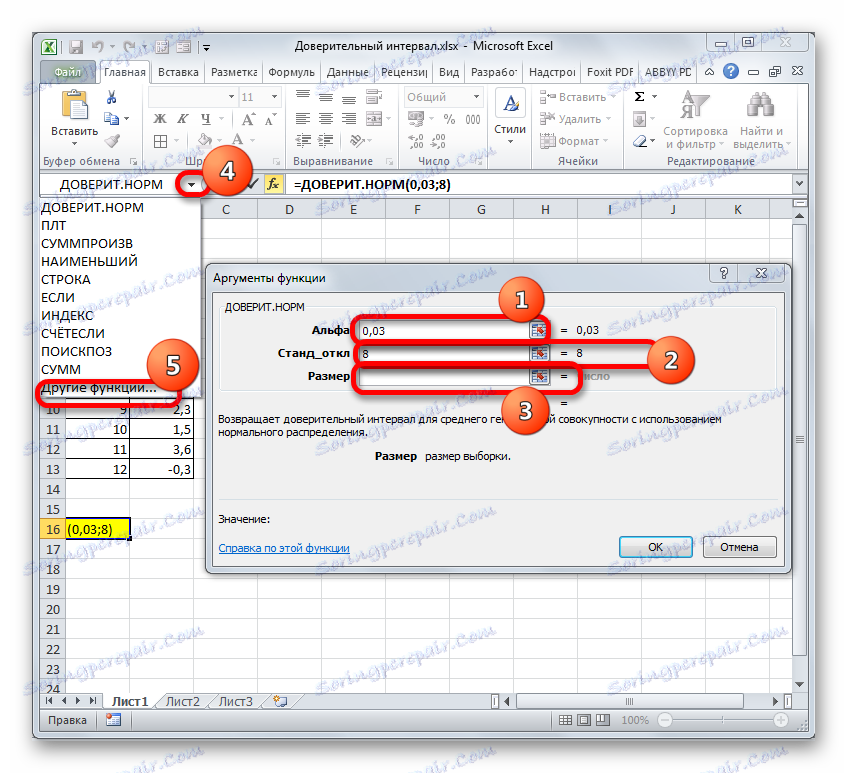
Задайте курсора на първото поле - "Alpha" . Тук трябва да посочим нивото на значимост. Както си спомняме, нивото на доверие в нас е 97%. В същото време казахме, че се изчислява по следния начин:(1-«Альфа»)*100Така че, за да се изчисли нивото на значимост, т.е. да се определи стойността на "Алфа", трябва да приложите формула от този вид:
(1-уровень доверия)/100Тоест, замествайки стойността, получаваме:
(1-97)/100Чрез прости изчисления научаваме, че аргументът "Алфа" е 0,03 . Въведете тази стойност в полето.
Както е известно, по подразбиране стандартното отклонение е 8 . Ето защо в полето "Стандартно отклонение" трябва само да напишете този номер.
В полето "Размер" трябва да въведете броя елементи на тестовете. Както си спомняме, има 12 от тях. Но за да автоматизираме формулата и да не я редактираме всеки път, когато се изпълнява нов тест, нека да зададем тази стойност не с обикновен номер, а с помощта на оператора COUNT . Така че, поставете курсора в полето "Размер" и кликнете върху триъгълника, който се намира отляво на формулата за формула.
Появява се списък с наскоро използваните функции. Ако наскоро бе приложено изказването COUNT , то трябва да е в този списък. В този случай просто трябва да кликнете върху името му. В противен случай, ако не го намерите, отидете на елемента "Други функции ..." .
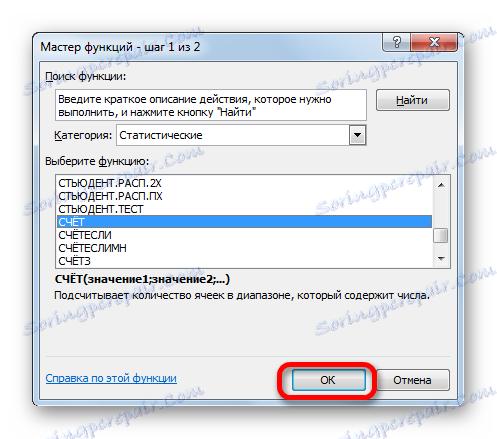
- Появява се вече познатият помощник за функциите . Отново отиваме в групата "Статистика" . Ние разпределяме там името "ACCOUNT" . Кликнете върху бутона "OK" .
- Появява се прозорецът с аргументи за горното изявление. Тази функция е предназначена да изчисли броя на клетките в определен диапазон, които съдържат числови стойности. Синтаксисът е:
=СЧЁТ(значение1;значение2;…)Групата с аргументи "Стойности" е препратка към диапазона, в който искате да изчислите броя клетки, попълнени с цифрови данни. Може да се броят до 255 такива аргумента, но в нашия случай ще е нужна само една.
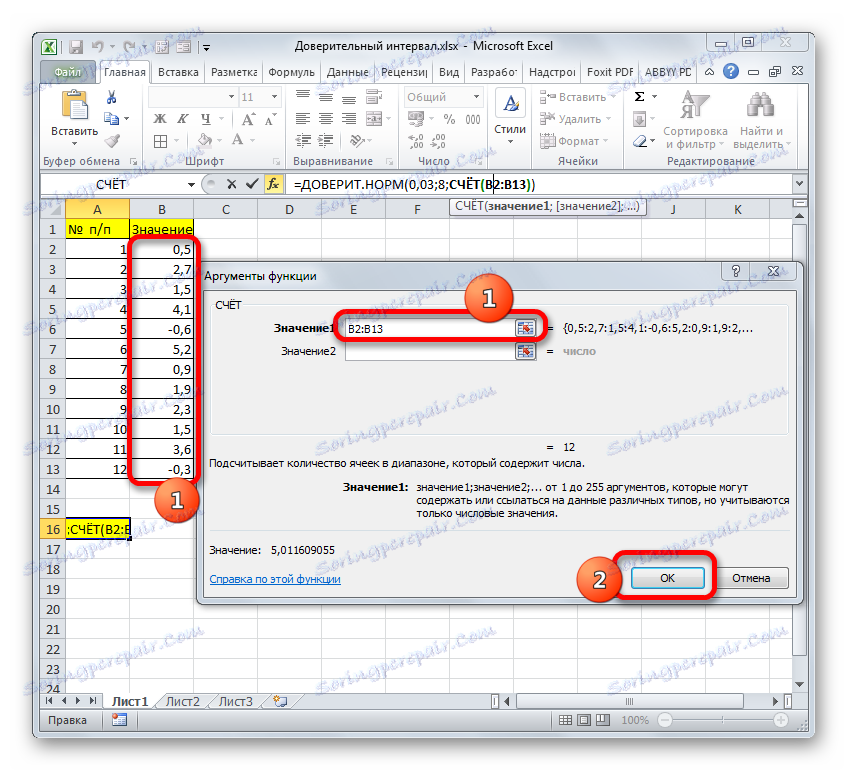
Задайте курсора в полето "Стойност1" и, като задържите левия бутон на мишката, изберете в листа диапазона, който съдържа нашата съвкупност. Тогава неговият адрес ще бъде показан на полето. Кликнете върху бутона "OK" .
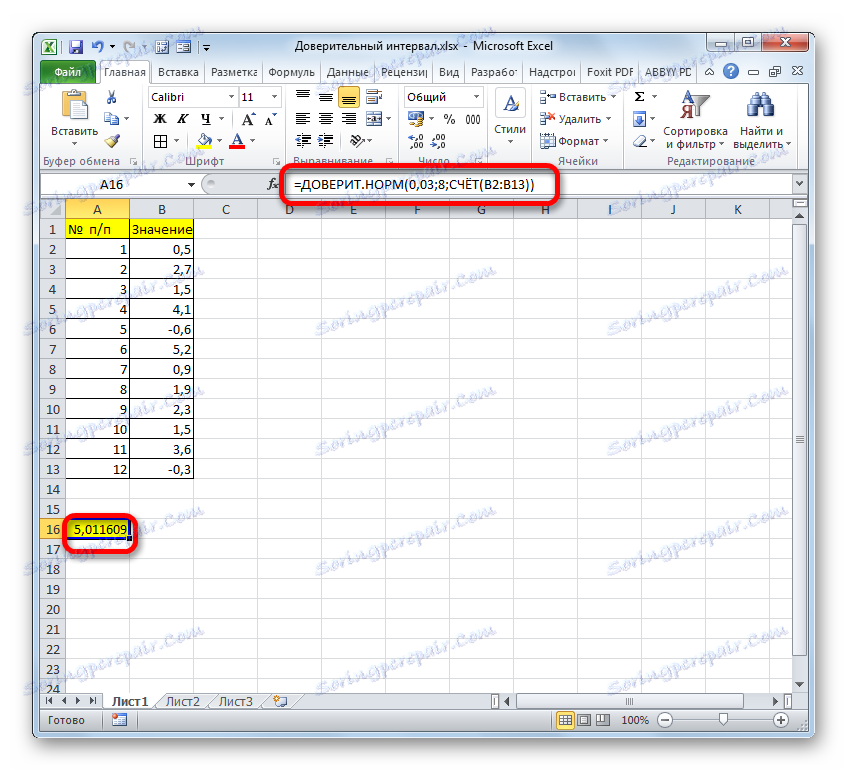
- След това приложението ще извърши изчислението и ще доведе резултата до клетката, в която се намира. В нашия конкретен случай формулата е следната:
=ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))Общият резултат от изчисленията е 5.011609 .
- Но това не е всичко. Както си спомняме, границата на доверителния интервал се изчислява чрез добавяне и изваждане от средната стойност на пробата на резултата от изчисляването на BIND.NORM . По този начин, съответно, се изчисляват десните и левите граници на доверителния интервал. Средната стойност на вземане на проби може да се изчисли с помощта на оператора AVERAGE .
Този оператор е предназначен да изчисли средноаритметичната стойност на избрания диапазон от номера. Той има следния сравнително прост синтаксис:
=СРЗНАЧ(число1;число2;…)Аргументът "брой" може да бъде или единична цифрова стойност, или позоваване на клетки или дори цели диапазони, които ги съдържат.
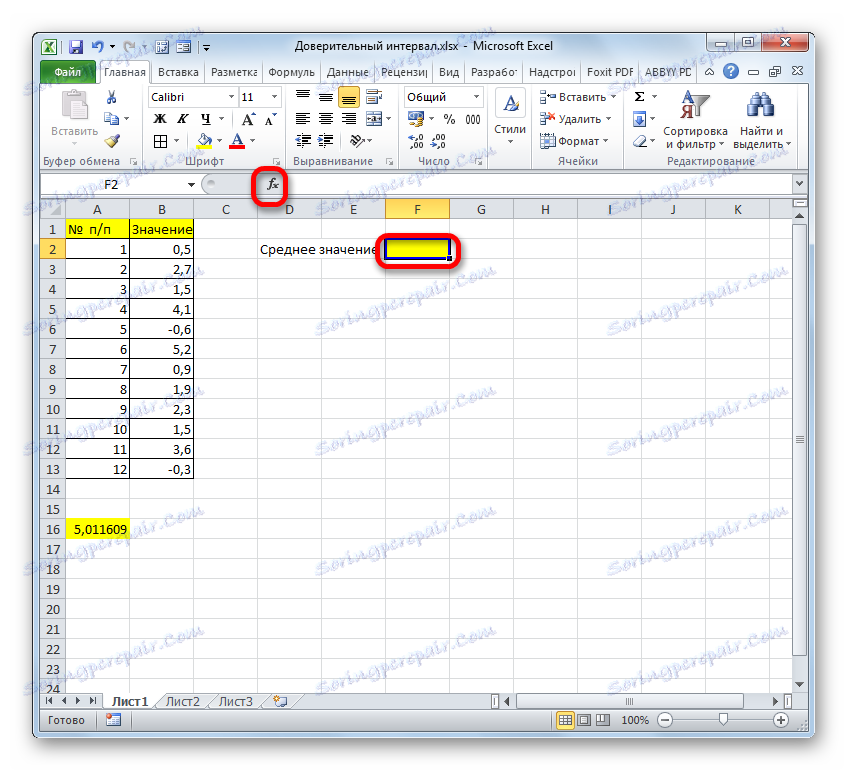
Така че, изберете клетката, в която ще се показва средната стойност, и кликнете върху бутона "Вмъкване на функция" .
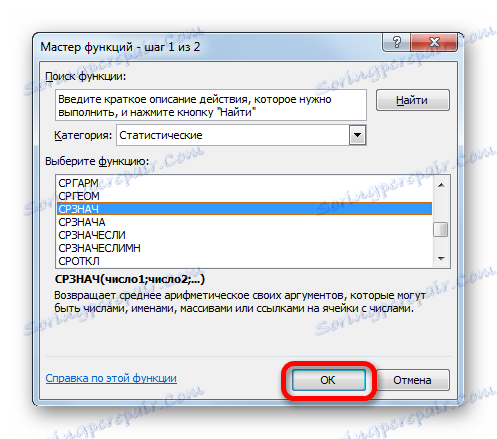
- Ще се отвори съветникът за функциите . Отново отидете в категорията "Статистика" и изберете от списъка името "СРЕДНО" . Както винаги, кликнете върху бутона "OK" .
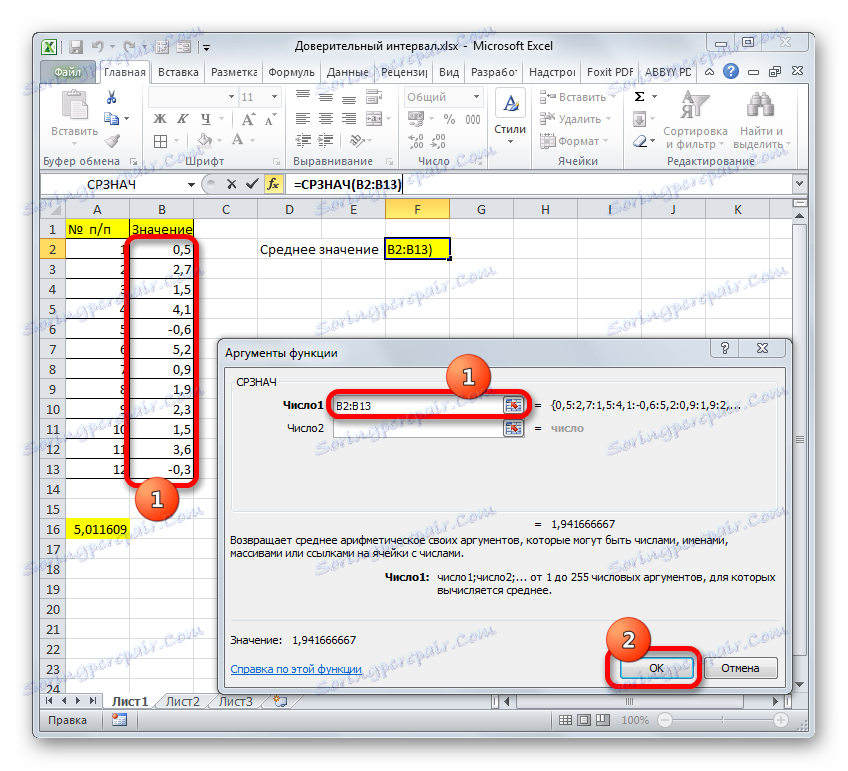
- Прозорецът с аргументи започва. Задайте курсора в полето "Номер 1" и изберете целия диапазон от стойности, като натиснете левия бутон на мишката. След като координатите се показват в полето, кликнете върху бутона "OK" .
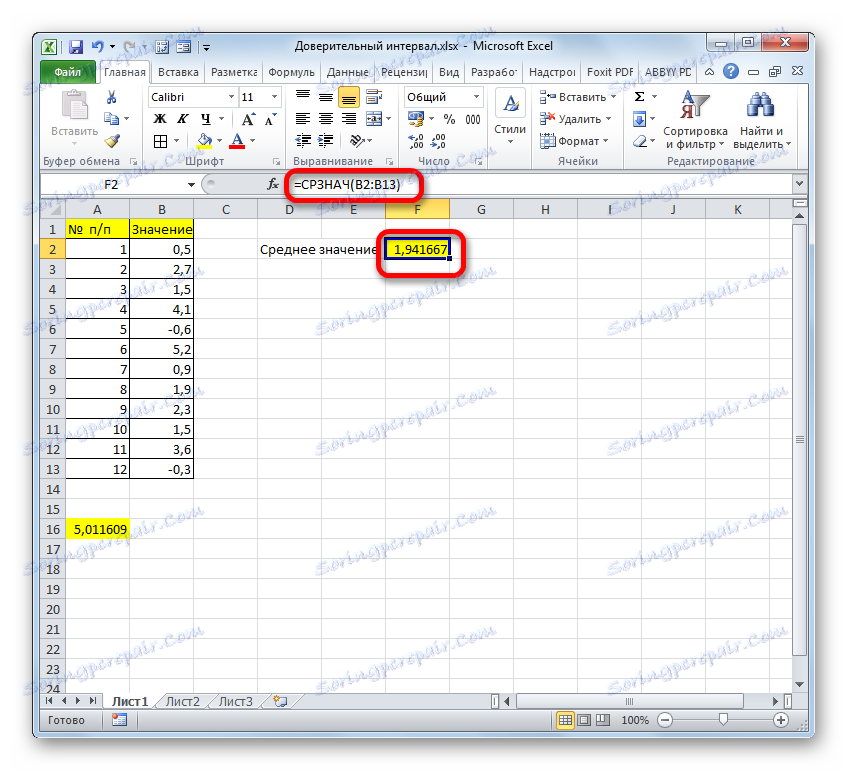
- След това AVERAGE показва резултата от изчислението в листовия елемент.
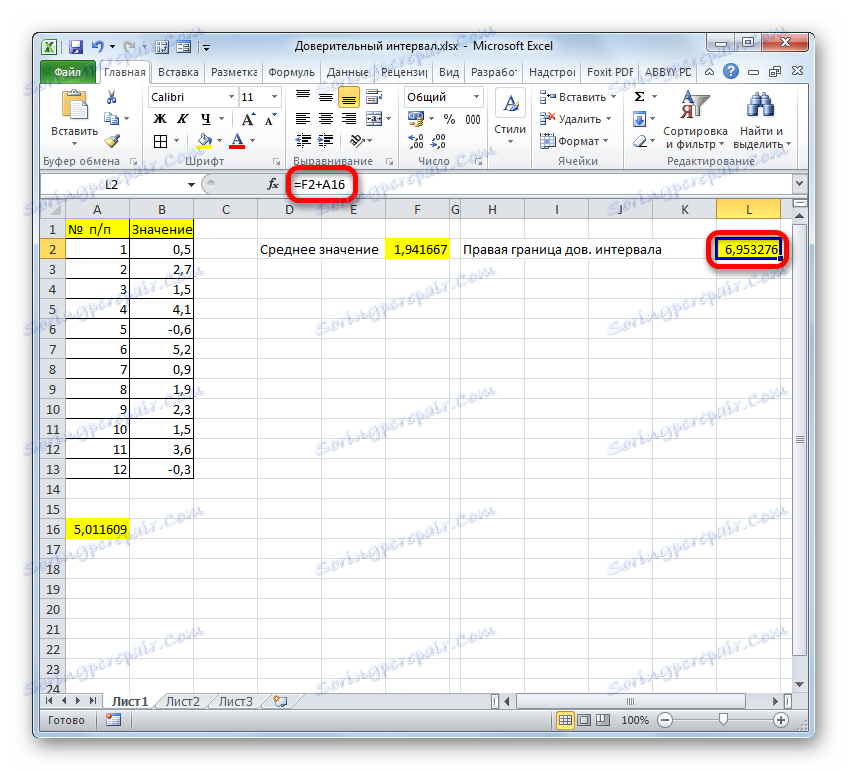
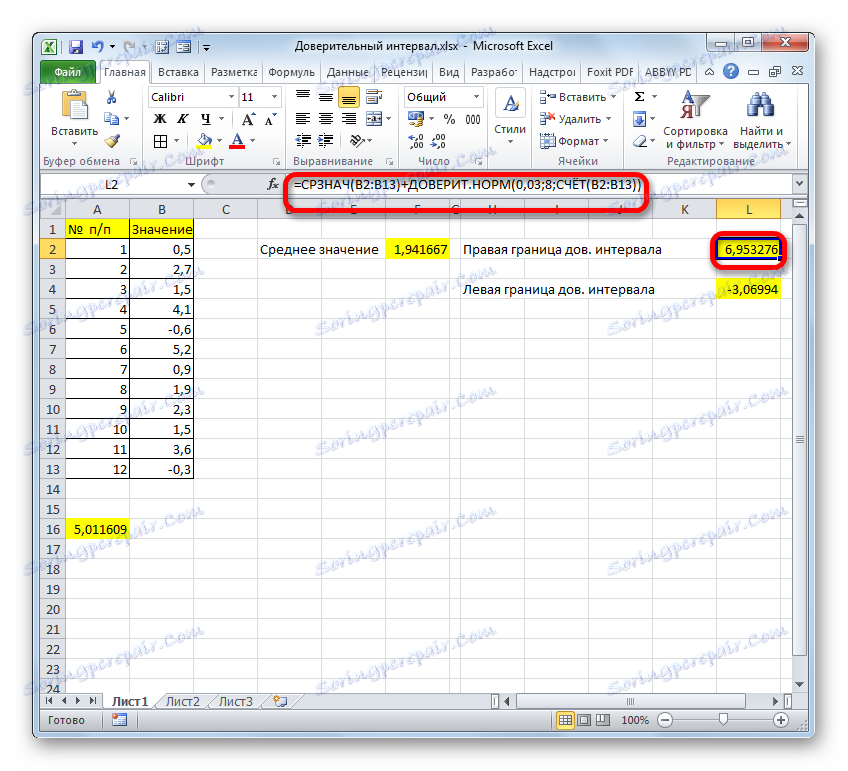
- Ние изчисляваме правилната граница на доверителния интервал. За да направите това, изберете отделна клетка, поставете знака "=" и добавете съдържанието на листовите елементи, в които се получават резултатите от изчисляването на функциите AVERAGE и TRUST . За да извършите изчислението, натиснете клавиша Enter . В нашия случай е получена следната формула:
=F2+A16Резултат от изчислението: 6,953276
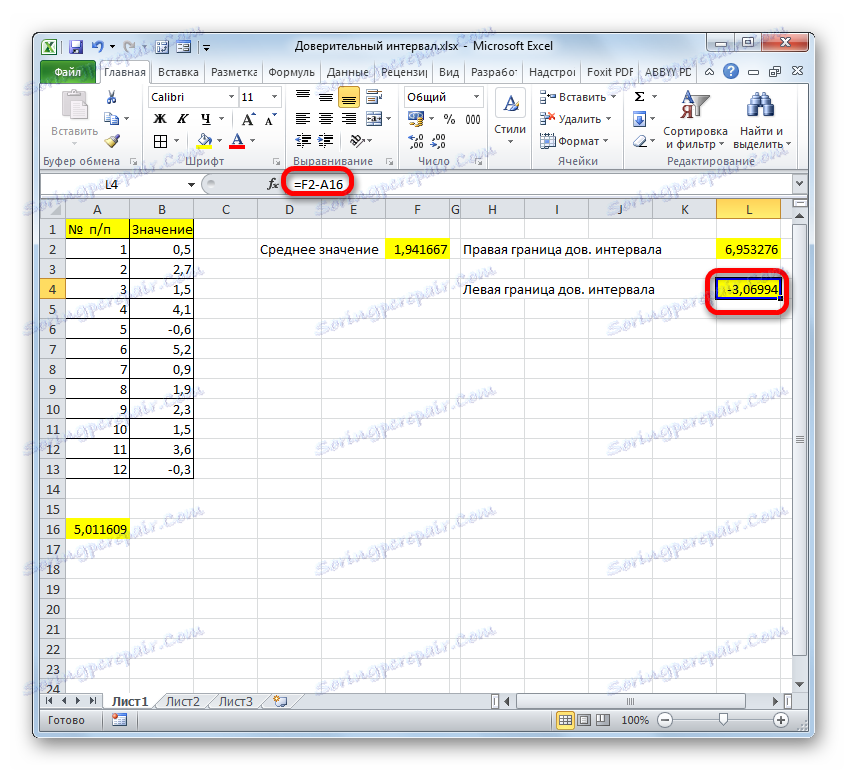
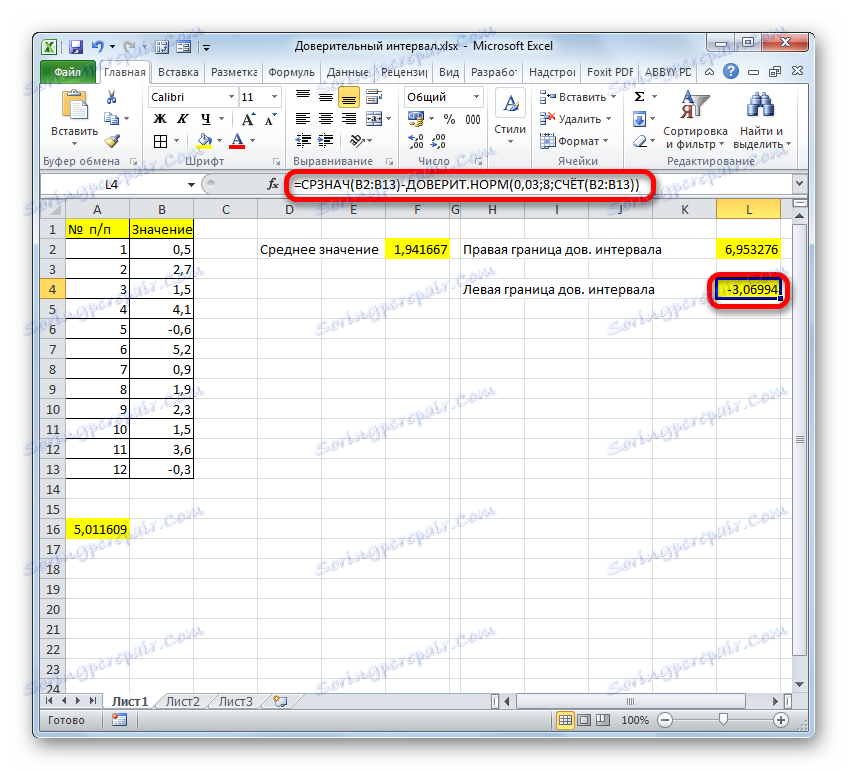
- По същия начин изчисляваме и лявата граница на доверителния интервал, само този път от резултата от изчислението на AVERAGE изваждаме резултата от изчислението на оператора TRUE . Формулата се получава за нашия пример от следния тип:
=F2-A16Резултатът от изчислението е -3,06994
- Опитахме се да опишем подробно всички действия за изчисляване на доверителния интервал, така че ние изписвахме всяка формула подробно. Но можете да комбинирате всички действия в една формула. Изчисляването на дясната граница на доверителния интервал може да бъде написано, както следва:
=СРЗНАЧ(B2:B13)+ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13)) - Подобно изчисление на лявата граница ще изглежда така:
=СРЗНАЧ(B2:B13)-ДОВЕРИТ.НОРМ(0,03;8;СЧЁТ(B2:B13))
Метод 2: Функцията TRUST BUDGET
Освен това има още една функция в Excel, която е свързана с изчисляването на доверителния интервал - DOVERIT.STUDENT . Изглежда, че започва само от Excel 2010. Този оператор извършва изчисляването на доверителния интервал на населението, използвайки разпределението на студентите. Много е удобно да се използва в случаите, когато вариацията и съответно стандартното отклонение са неизвестни. Синтаксисът на оператора е:
=ДОВЕРИТ.СТЬЮДЕНТ(альфа;стандартное_откл;размер)
Както можете да видите, имената на операторите останаха непроменени в този случай.
Да видим как да изчислим границите на доверителен интервал с неизвестно стандартно отклонение въз основа на примера на същия агрегат, който взехме предвид при предишния метод. Нивото на доверие, както и последният път, ще вземем 97%.
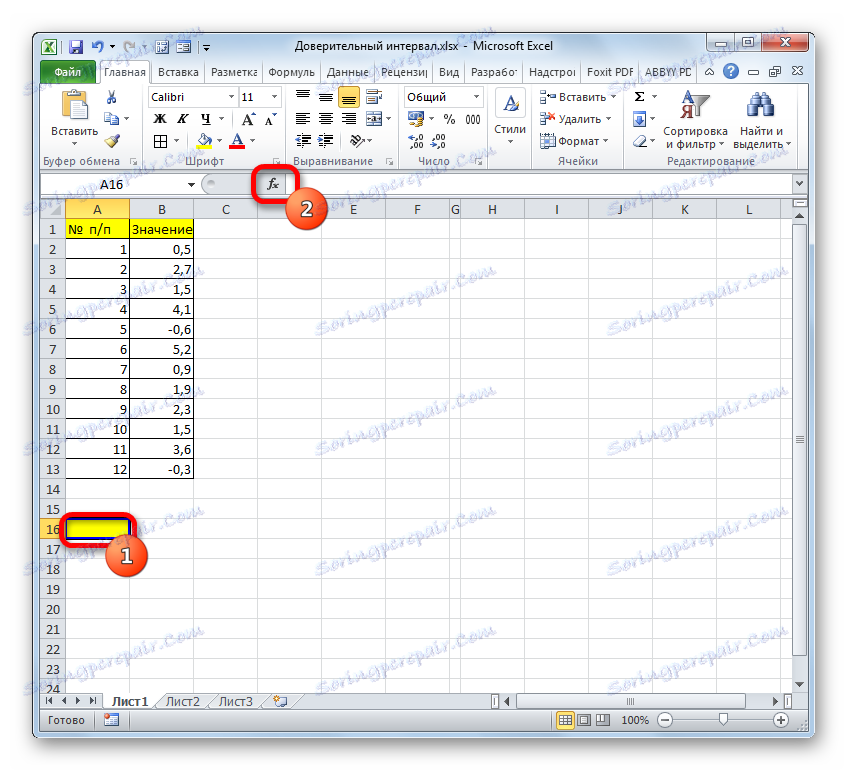
- Изберете клетката, в която ще бъде направено изчислението. Кликваме върху бутона "Вмъкване на функция" .
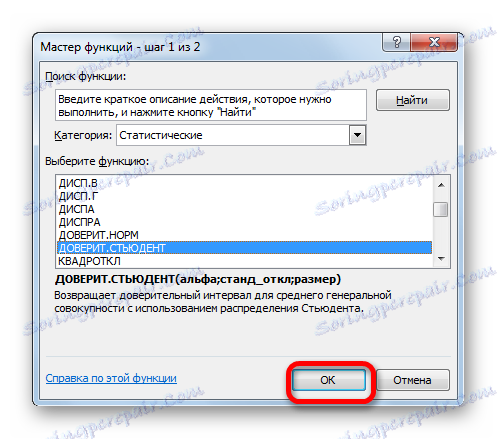
- В отворения магистър на функциите преминаваме към категорията "Статистически" . Избираме името "Доверие". Кликнете върху бутона "OK" .
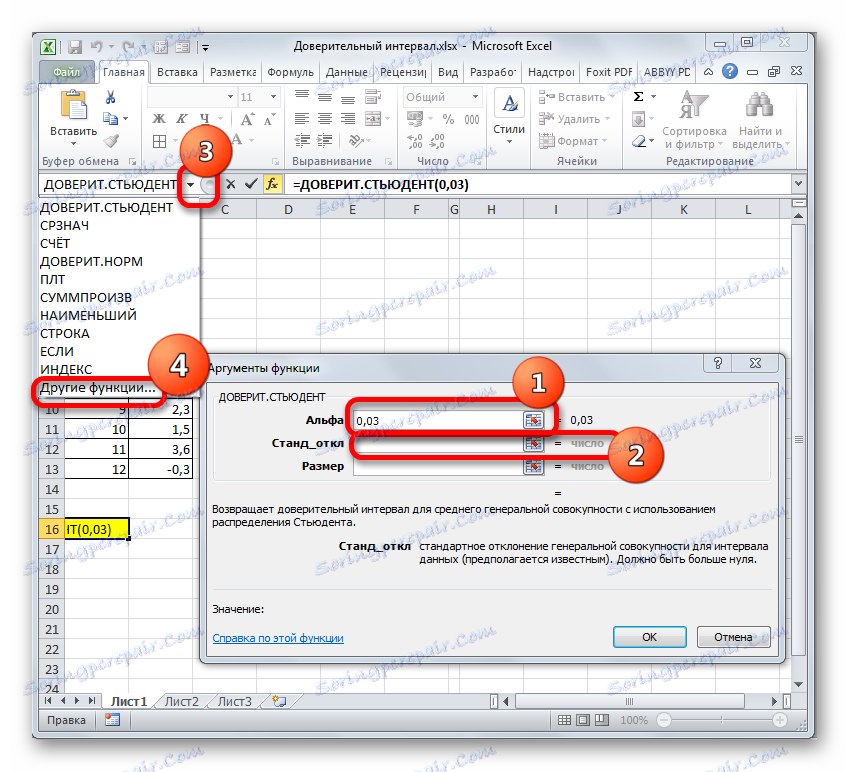
- Отваря се прозорецът с аргументи на посочения оператор.
В полето "Alpha" , като се има предвид, че нивото на доверие е 97%, напишете числото 0.03 . Вторият път по принципите на изчисляване на този параметър няма да се задържаме.
След това задайте курсора в полето "Стандартно отклонение" . Този път този индикатор е неизвестен за нас и трябва да бъде изчислен. Това се прави с помощта на специална функция - STD . За да се обадите на прозореца на този оператор, кликнете върху триъгълника отляво на формулата. Ако не открием желаното име в списъка, който се отваря, отиваме в елемента "Други функции ..." .
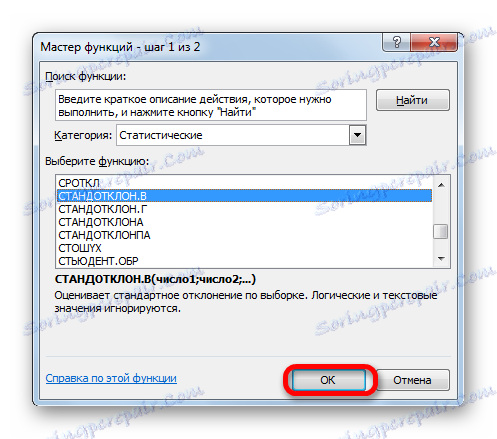
- Стартира съветникът за функции . Преминаваме в категорията "Статистически" и маркираме името "STANDOTKLON.V" в него. След това кликнете върху бутона "OK" .
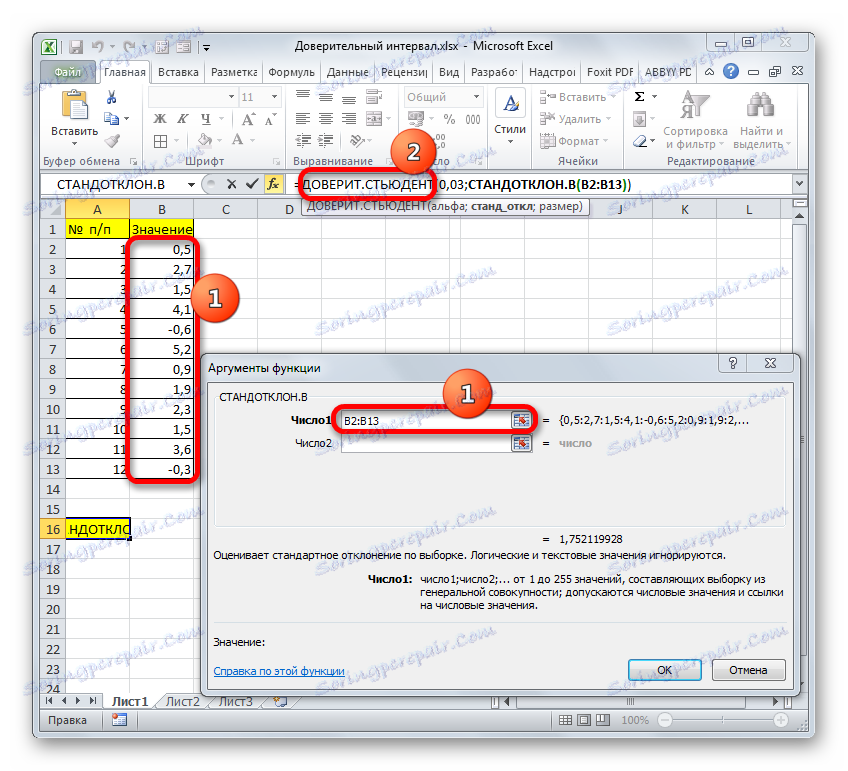
- Отваря прозореца с аргументи. Задачата на оператора на STDEV е да определи стандартното отклонение в извадката. Синтаксисът му изглежда така:
=СТАНДОТКЛОН.В(число1;число2;…)Не е трудно да се предположи, че аргументът "Номер" е адреса на елемента за избор. Ако пробата е поставена в един масив, можете да използвате един аргумент, за да отнесете този диапазон.
Задайте курсора в полето "Номер 1" и винаги, като държите левия бутон на мишката, изберете колекцията. След като координатите са в полето, не бързайте да натискате бутона "OK" , тъй като резултатът ще се окаже неправилен. Първо, трябва да се върнем към прозореца с аргументи на оператора TRUST.STUDENT , за да направим последния аргумент. За целта кликнете върху съответното име в лентата за формули.
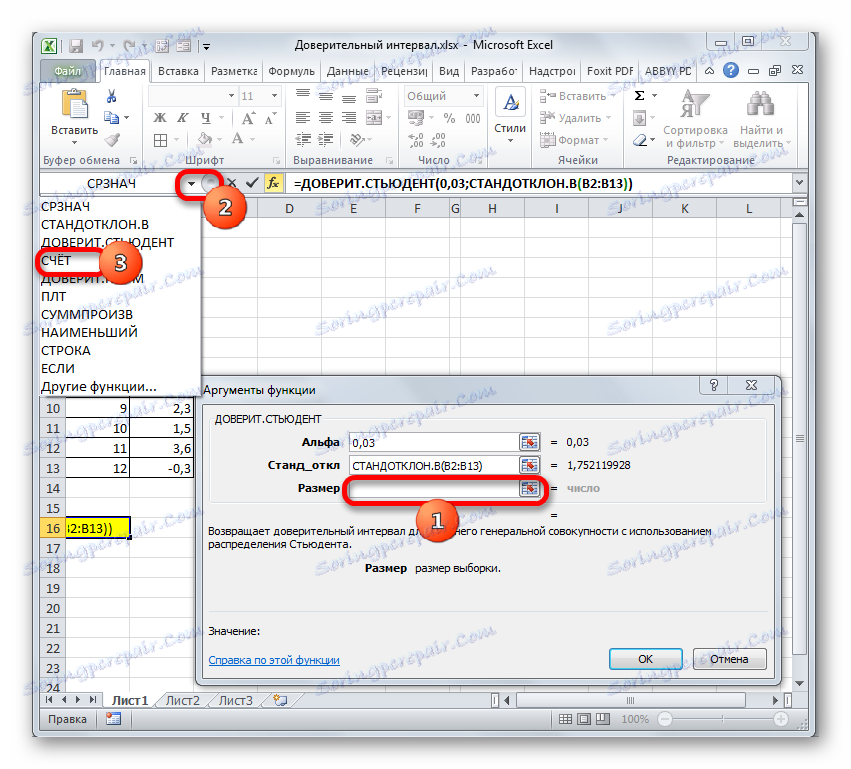
- Прозорецът на аргументите на вече познатата функция се отваря отново. Задайте курсора в полето "Размер" . Отново кликнете върху вече познатия триъгълник, за да отидете на избора на оператори. Както разбирате, имаме нужда от името "ACCOUNT" . Тъй като ние използвахме тази функция за изчисления в предишния метод, тя присъства в този списък, така че просто кликнете върху него. Ако не го намерите, следвайте алгоритъма, описан в първия метод.
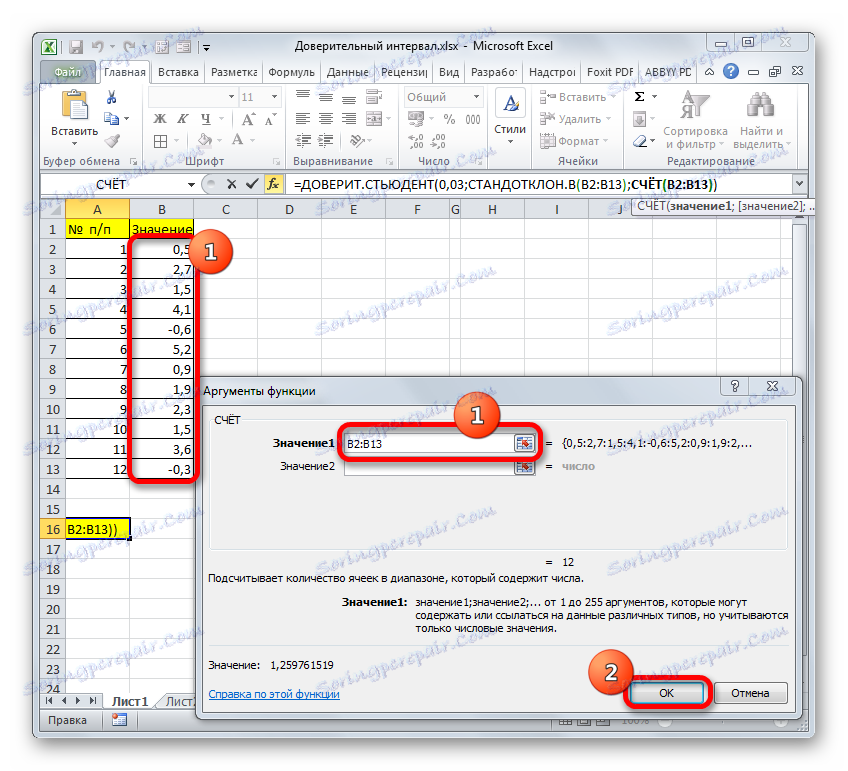
- След като в прозореца на аргументите ACCOUNT поставете курсора в полето "Номер 1" и изберете комплекта с натиснат бутон на мишката. След това кликнете върху бутона "OK" .
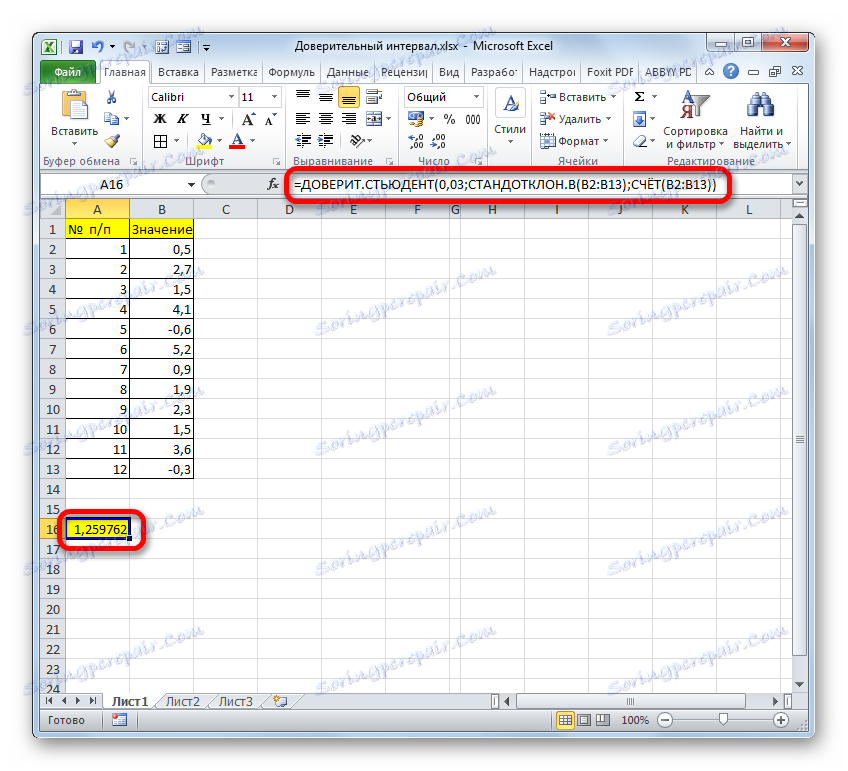
- След това програмата изчислява и показва стойността на доверителния интервал.
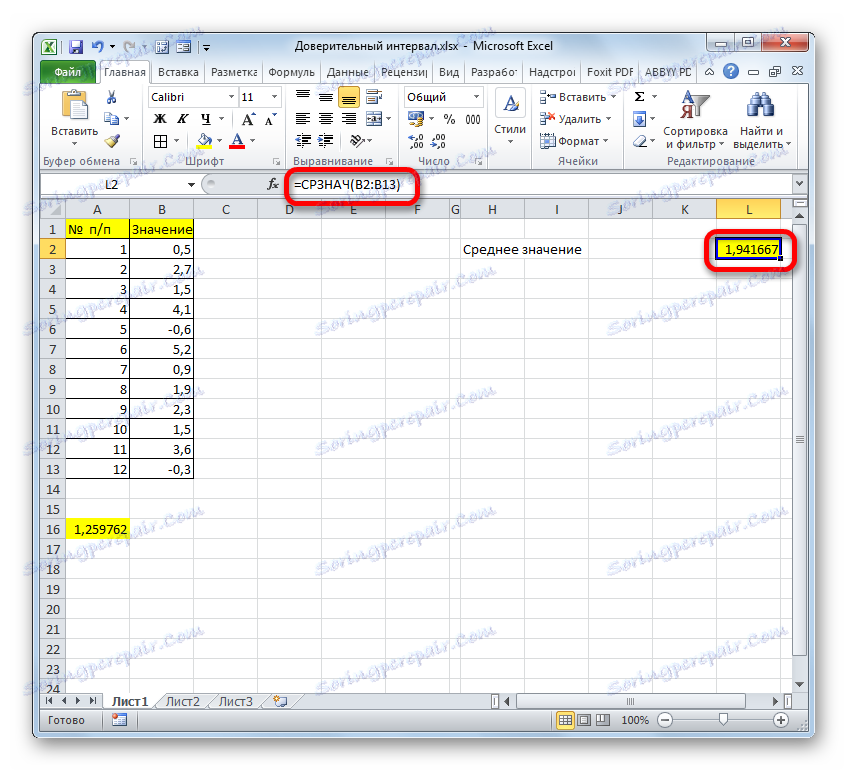
- За да определим границите, отново трябва да изчислим средната стойност на пробата. Но, като се има предвид, че алгоритъмът на изчисление, използвайки формулата AVERAGE, е същият като в предишния метод и дори резултатът не се е променил, няма да се занимаваме с това подробно за втори път.
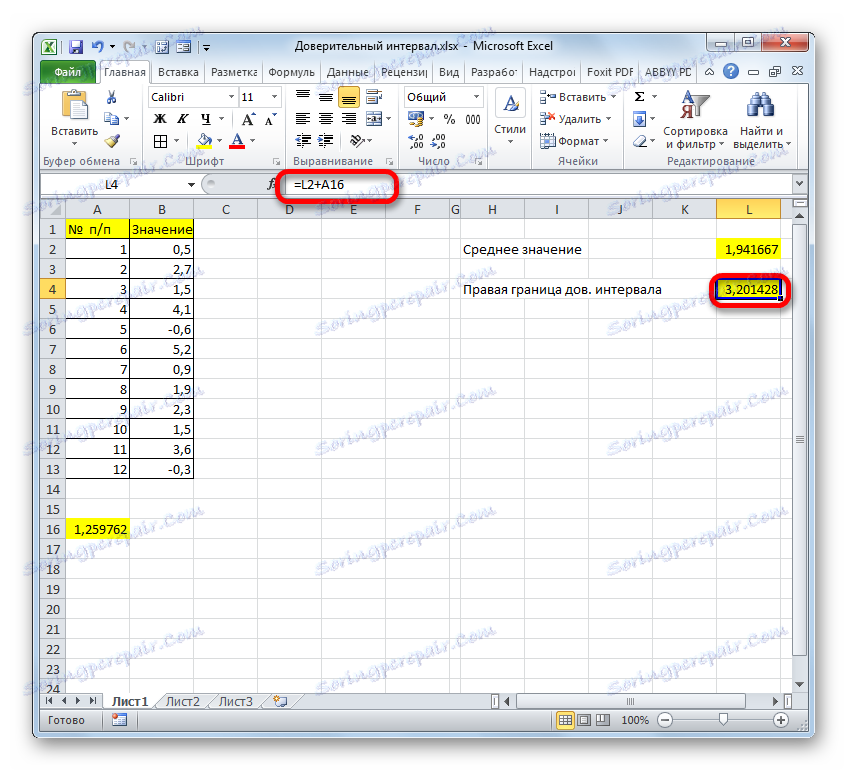
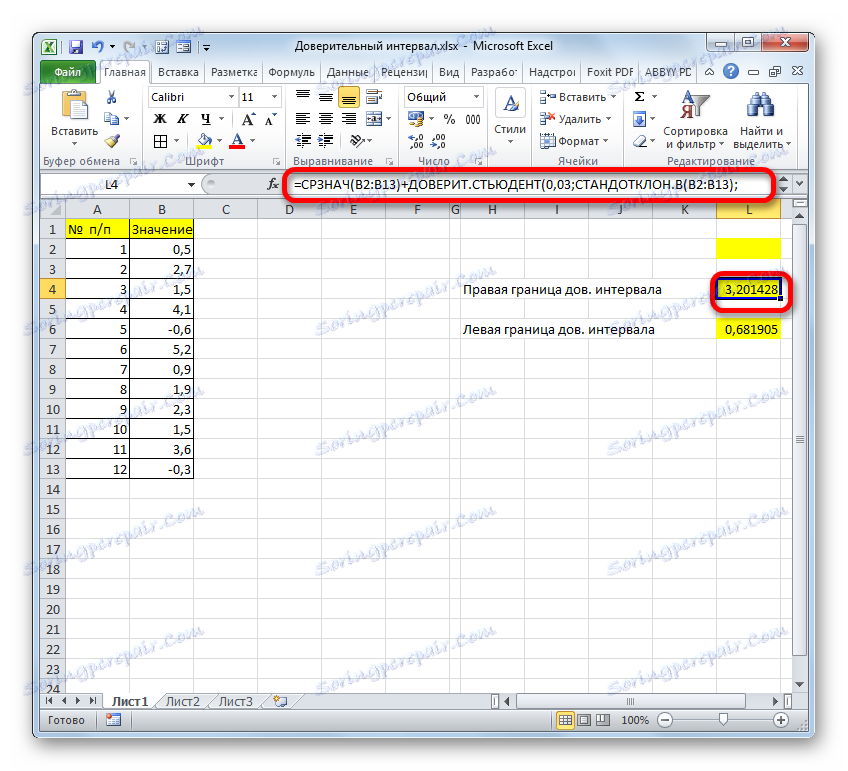
- Съчетавайки резултатите от изчисляването на AVERAGE и TRUST , получаваме правилната граница на доверителния интервал.
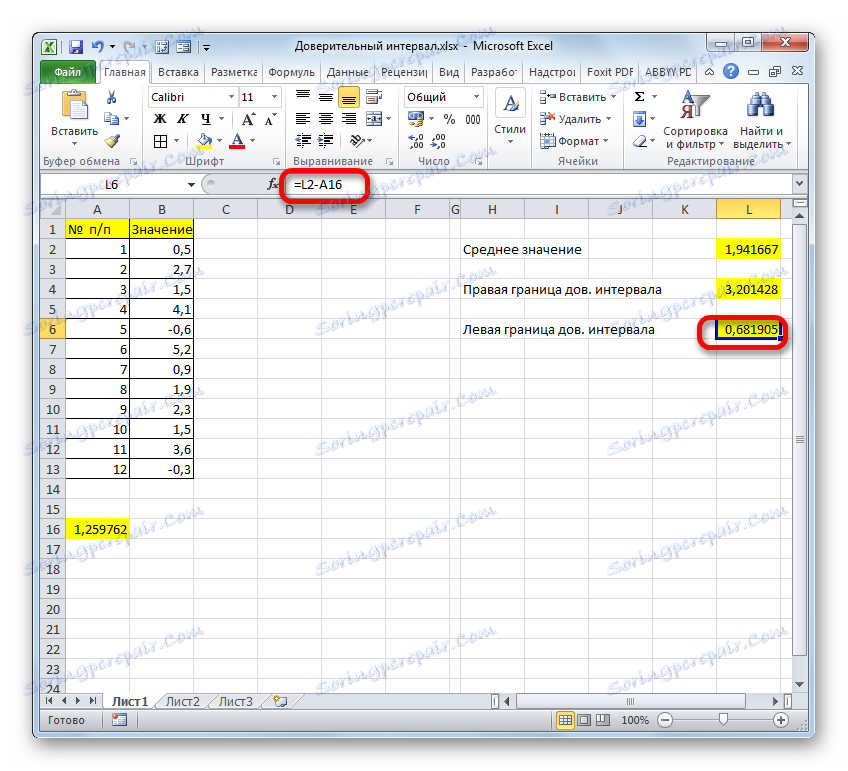
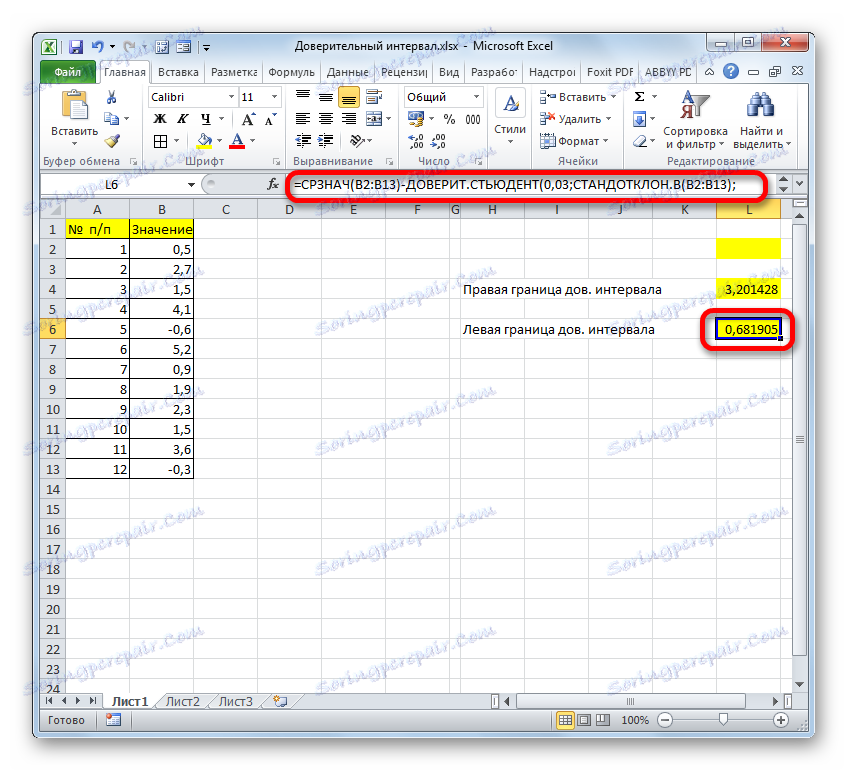
- След като извадихме от резултатите от изчисляването на оператора AVERAGE резултата от изчисляването на TRUSTENT , имаме лявата граница на доверителния интервал.
- Ако изчислението е написано с една формула, изчисляването на десните граници в нашия случай ще изглежда така:
=СРЗНАЧ(B2:B13)+ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13)) - Съответно формулата за изчисляване на лявата граница ще изглежда така:
=СРЗНАЧ(B2:B13)-ДОВЕРИТ.СТЬЮДЕНТ(0,03;СТАНДОТКЛОН.В(B2:B13);СЧЁТ(B2:B13))
Както можете да видите, инструментите на програмата Excel правят много по-лесно изчисляването на доверителния интервал и неговите граници. За тези цели се използват отделни оператори за проби, при които вариацията е известна и неизвестна.