Изчисляване на коефициента на вариация в Microsoft Excel
Един от основните статистически показатели за последователност от номера е коефициентът на вариация. За да го намерите, са направени доста сложни изчисления. Инструментите на Microsoft Excel го правят много по-лесно за потребителя.
съдържание
Изчисляване на коефициента на вариация
Това е съотношението на стандартното отклонение към средната аритметична стойност. Резултатът се изразява като процент.
В Excel няма отделна функция за изчисляване на този показател, но съществуват формули за изчисляване на стандартното отклонение и средната аритметика на определен брой числа, а именно, те се използват за намиране на коефициент на вариация.
Стъпка 1: Изчислете стандартното отклонение
Стандартното отклонение или, както се нарича по друг начин, стандартното отклонение, е квадратният корен на дисперсия , За да изчислите стандартното отклонение, използвайте функцията STDEV . Започвайки с версията на Excel 2010, тя се разделя на две отделни версии: STANDOTTKLON.G и STANDOTKLON.V , в зависимост от това дали популацията е изчислена или взета проба според пробата.
Синтаксисът на тези функции изглежда така:
= СТАНДОТКЛОН(Число1;Число2;…)
= СТАНДОТКЛОН.Г(Число1;Число2;…)
= СТАНДОТКЛОН.В(Число1;Число2;…)
- За да изчислите стандартното отклонение, изберете която и да е свободна клетка на листа, която е удобна, за да покажете резултатите от изчисленията в нея. Кликваме върху бутона "Вмъкване на функция" . Той има вида на иконата и се намира отляво на формулата.
- Активирането на функцията Wizard се изпълнява, което започва като отделен прозорец със списък от аргументи. Да отидем в категорията "Статистически" или "Пълен азбучен списък" . Избираме името "STANDOTTKLON.G" или "STANDOTKLON.V" , в зависимост от това дали трябва да се изчисли популацията или пробата. Кликнете върху бутона "OK" .
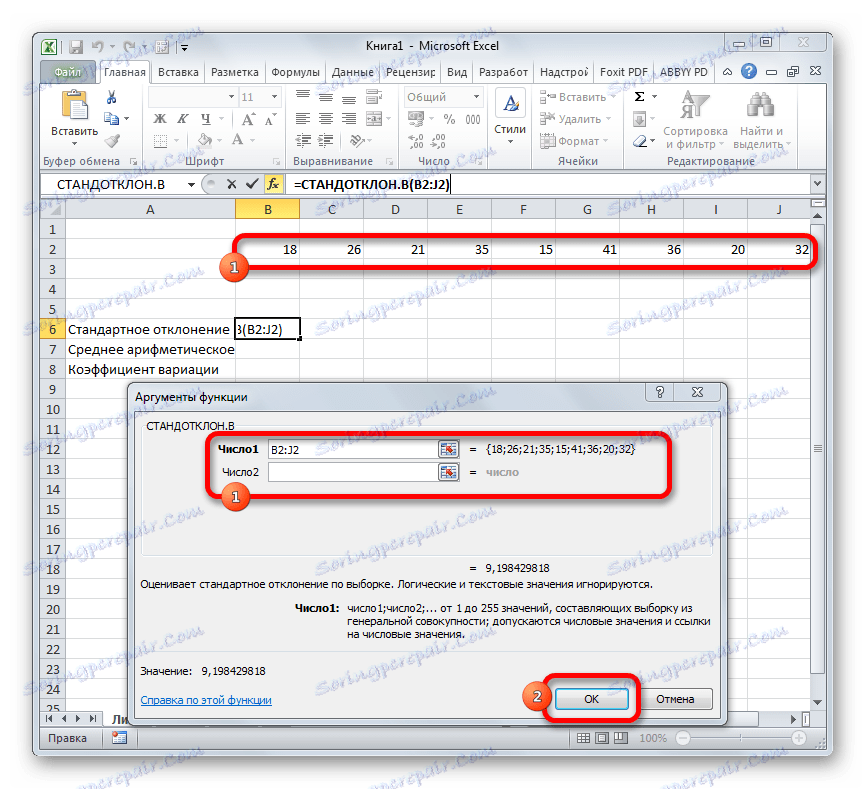
- Отваря прозореца с аргументи за тази функция. Той може да има от 1 до 255 полета, които могат да съдържат както конкретни номера, така и връзки към клетки или диапазони. Поставяме курсора в полето "Номер1" . Мишката избира в листа диапазона от стойности, които трябва да бъдат обработени. Ако има няколко такива зони и те не са в съседство помежду си, то координатите на следващата точка в полето "Номер 2" и т.н. Когато всички необходими данни са въведени, кликнете върху бутона "OK"
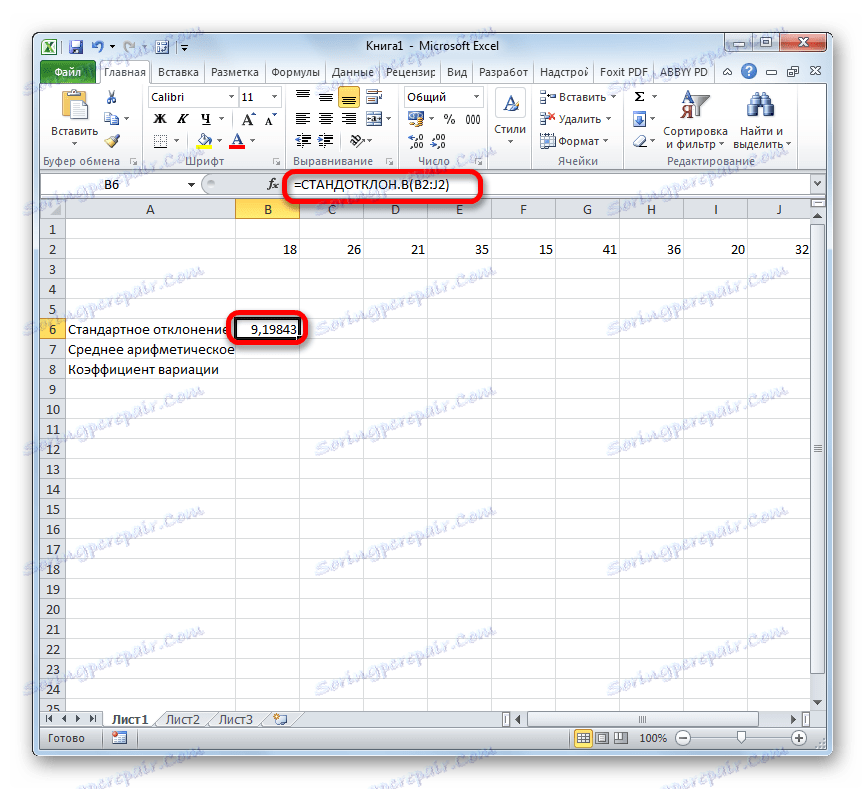
- В предварително разпределената клетка се показва резултата от изчислението на избрания тип стандартно отклонение.

Урокът: Формулата за стандартното отклонение в Excel
Стъпка 2: Изчислете аритметичната средна стойност
Аритметичната средна стойност е съотношението на общата сума от всички стойности на серийния номер към техния брой. За да изчислите този индикатор, има и отделна функция - СРЕДНО . Нека изчислим стойността си на конкретен пример.
- Изберете клетка в листа, за да покажете резултата. Кликнете върху вече познатия бутон "Вмъкване на функция" .
- В статистическата категория на съветника за функции търсим името "СРЕДНО" . След избора си, кликнете върху бутона "OK" .
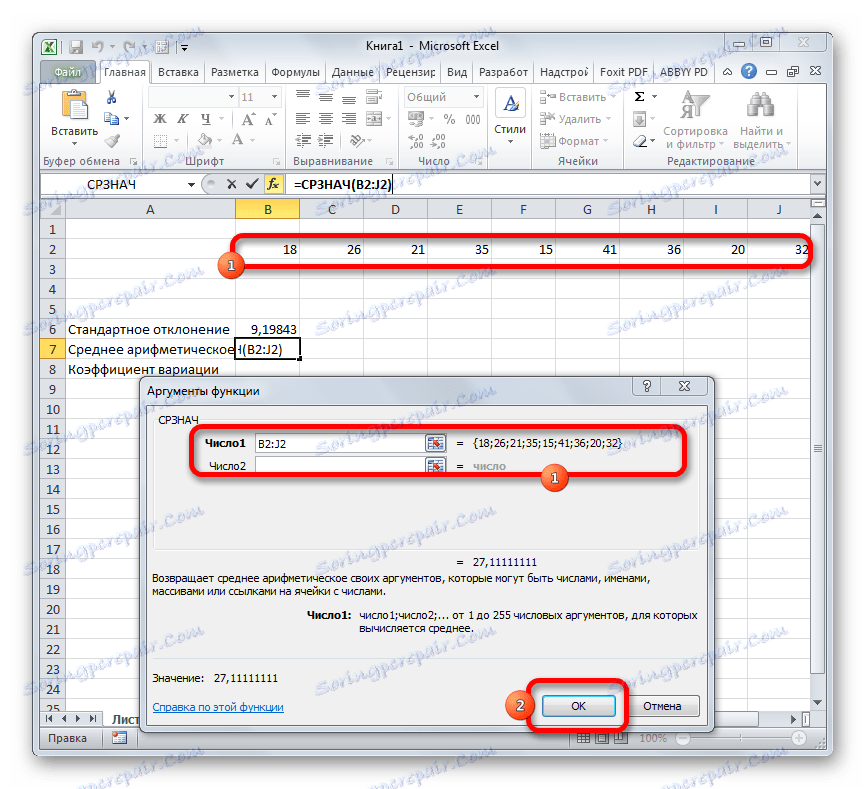
- Прозорецът за аргументи AVERAGE е стартиран . Аргументите са напълно идентични с тези на операторите на групата STDEV . Това означава, че в качеството им могат да действат като отделни числови стойности и референции. Задайте курсора в полето "Номер 1" . Точно както в предишния случай, ние избираме набор от клетки, които имаме нужда от листа. След като координатите им са въведени в полето на прозореца с аргументи, кликнете върху бутона "OK" .
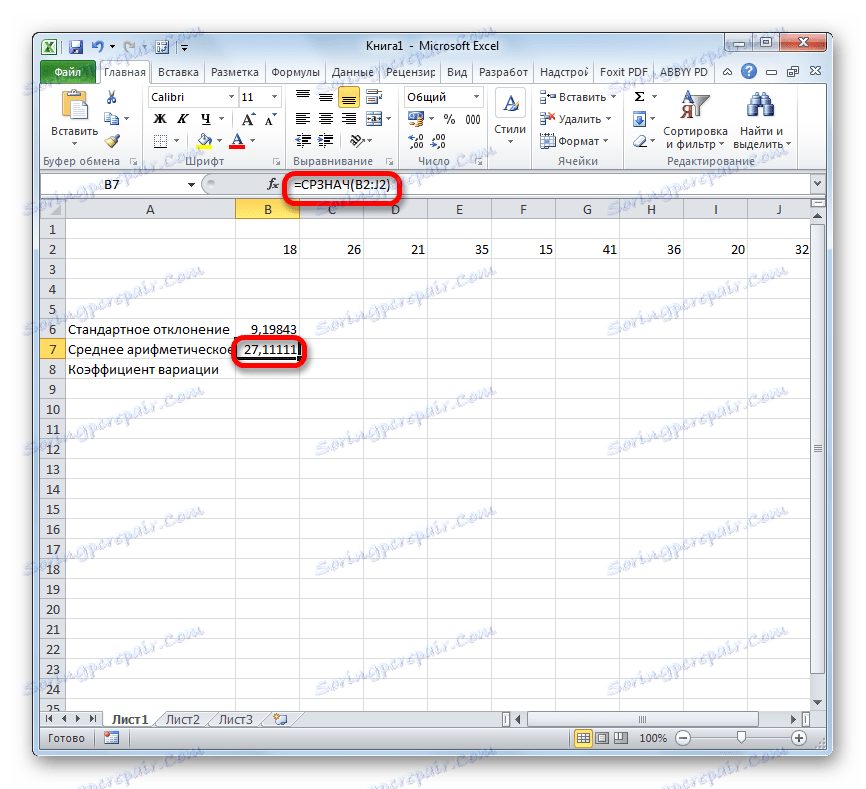
- Резултатът от изчисляването на средната аритметика се извежда към клетката, която е била избрана преди отварянето на съветника .
Урокът: Как да изчисляваме средната стойност в Excel
Стъпка 3: Намиране на коефициент на вариация
Сега разполагаме с всички необходими данни, за да изчислим директно коефициента на вариация.
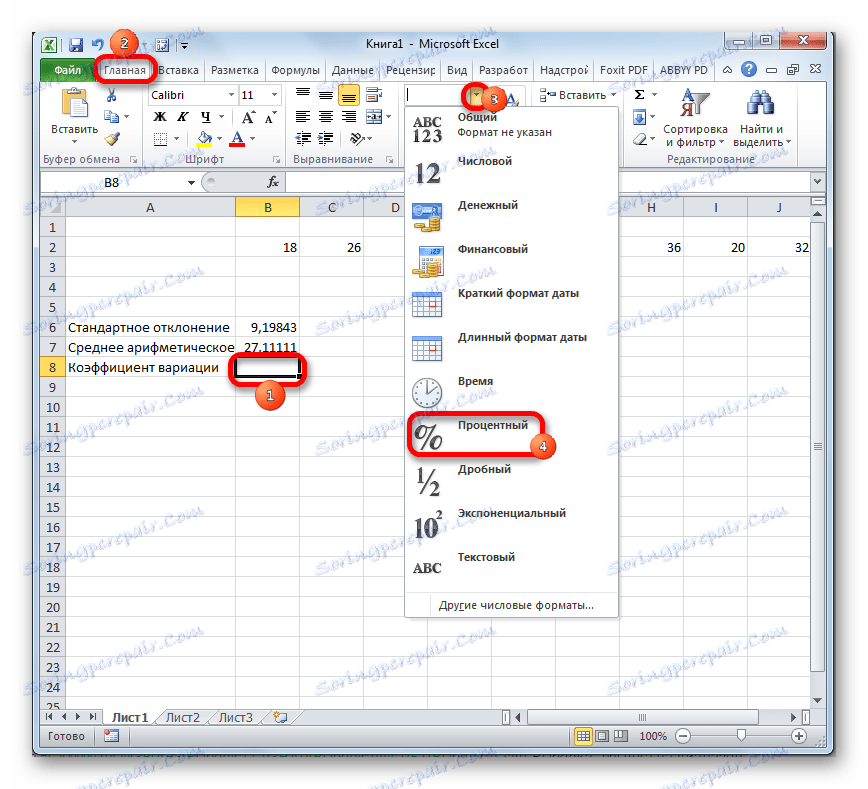
- Изберете клетката, в която ще се показва резултата. На първо място, трябва да вземете предвид, че коефициентът на вариация е процентна стойност. В тази връзка трябва да промените формата на клетката на съответната. Това може да стане след избора му, докато в раздела "Начало" . Кликнете върху полето на формата на лентата в полето "Номер" . От отворения списък с опции изберете "Интерес" . След тези действия форматът на елемента ще бъде съответстващ.
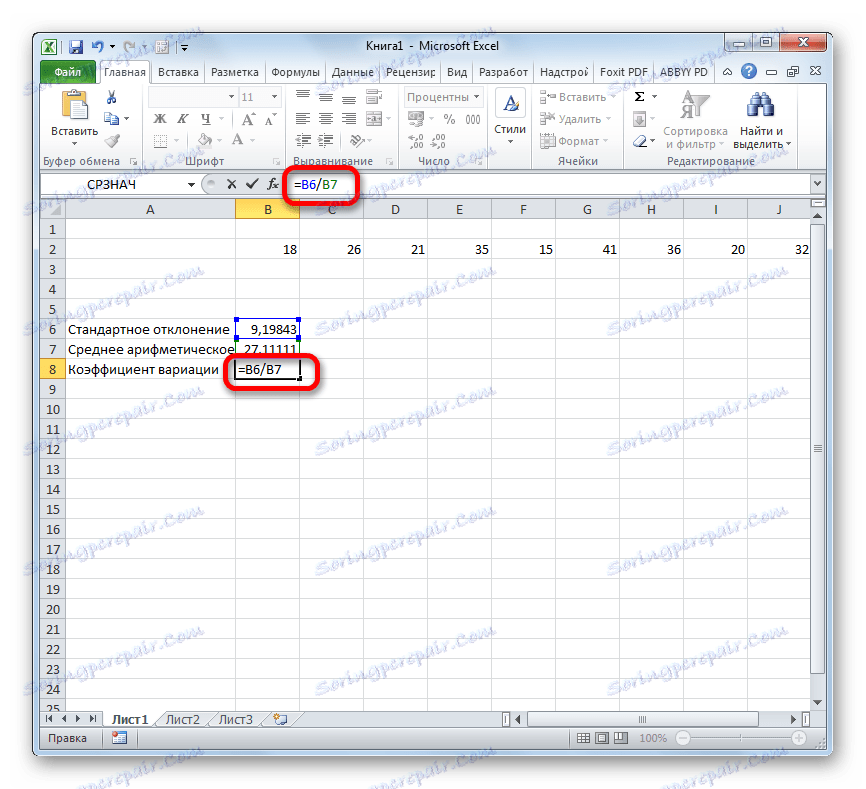
- Отново се върнете в клетката, за да покажете резултата. Активирайте го като кликнете два пъти върху левия бутон на мишката. Слагаме в него знака "=" . Изберете елемента, в който се намира общото изчисление на стандартното отклонение. Кликваме върху бутона "разделяне" (/) на клавиатурата. След това изберете клетката, в която се намира средната аритметична стойност на дадената цифрова серия. За да изчислите и покажете стойността, кликнете върху бутона Enter на клавиатурата.
- Както можете да видите, резултатът от изчислението се показва.
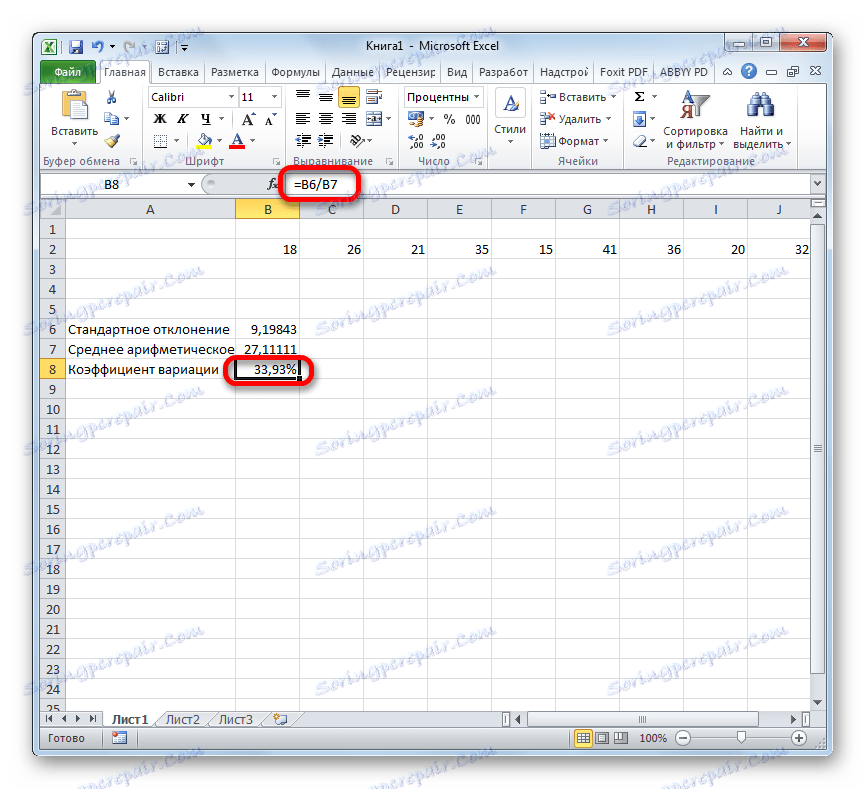
По този начин изчислихме коефициента на вариация, отнасящ се до клетките, в които са изчислени стандартното отклонение и средната аритметика. Но можете да направите малко по-различно, без да изчислявате данните поотделно.
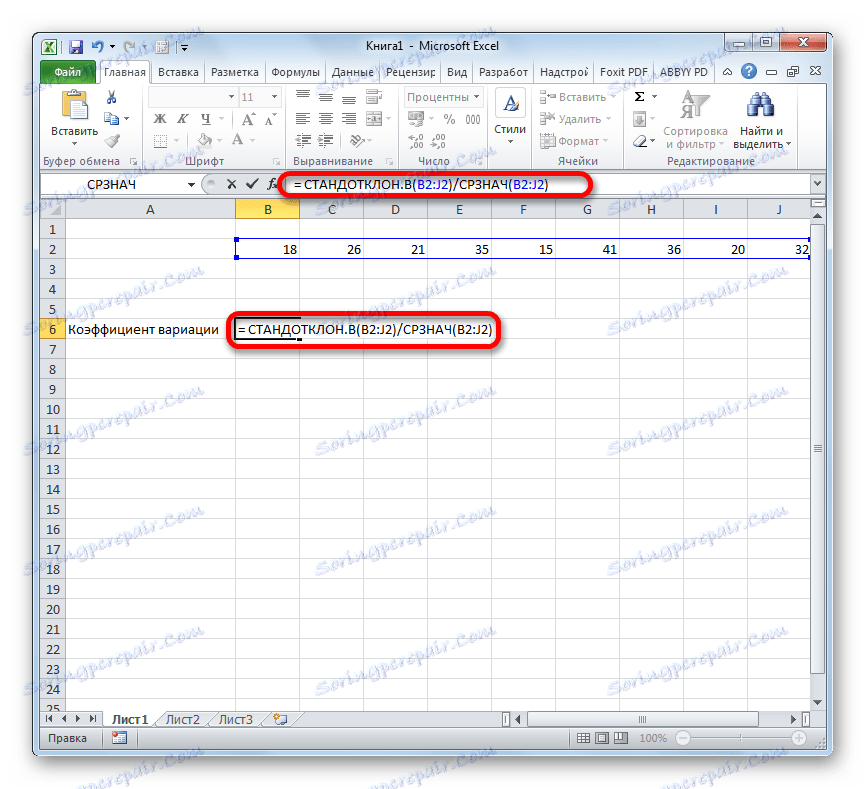
- Избираме клетката, предварително форматирана под процентния формат, в който ще се изведе резултатът. Напишете в него формула по тип:
= СТАНДОТКЛОН.В(диапазон_значений)/СРЗНАЧ(диапазон_значений)Вместо името "Value Range", вмъкваме истинските координати на областта, в която се намират изброените номера. Това може да стане, като просто изберете този диапазон. Вместо STDEV, ако потребителят сметне за необходимо, можете да използвате функцията STDEV .
- След това, за да изчислите стойността и да покажете резултата на екрана на монитора, кликнете върху бутона Enter .
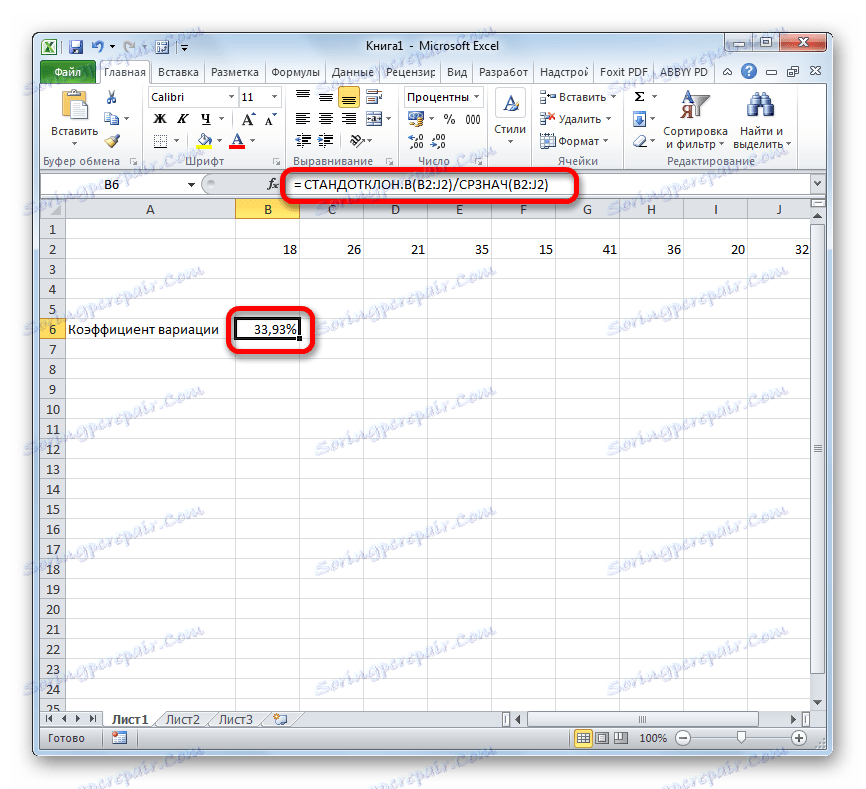
Има условна диференциация. Смята се, че ако коефициентът на коефициент на вариация е по-малък от 33%, тогава наборът от числа е хомогенен. В противен случай е обичайно да се характеризира като хетерогенна.
Както можете да видите, програмата Excel дава възможност значително да се опрости изчисляването на такова сложно статистическо изчисление като търсене на коефициент на вариация. За съжаление, приложението все още няма функция, която би изчислила този индикатор в едно действие, но с помощта на операторите STDEV и AVERAGE тази задача е много опростена. По този начин в Excel може да се извършва дори от човек, който няма високо ниво на познание, свързано със статистически модели.