Регресионен анализ в Microsoft Excel

Регресионният анализ е един от най-популярните методи за статистически изследвания. С негова помощ можете да определите степента на влияние на независимите променливи върху зависимата променлива. Във функционалността на Microsoft Excel съществуват инструменти, предназначени за извършване на този тип анализ. Нека да анализираме какви са и как да ги използваме.

Свързване на пакета за анализ

Но, за да използвате функция, която ви позволява да извършвате регресионен анализ, първо трябва да активирате пакета за анализ. Само тогава инструментите, необходими за тази процедура, ще се появят на лентата на Excel.

1. Преминаваме към раздела "Файл" .
2. Отворете раздела "Настройки" .
3. Отваря прозореца на опциите в Excel. Преминаваме към подраздел "Суперструктури" .
4. В най-долната част на прозореца, който се отваря, преместете превключвателя в блока "Управление" на позиция "Добавки в Excel" , ако е в различно положение. Кликнете върху бутона "Отиди" .
5. Отваря се прозорецът за наличните добавки в Excel. Поставете отметка в квадратчето "Пакет за анализ" . Кликнете върху бутона "OK".

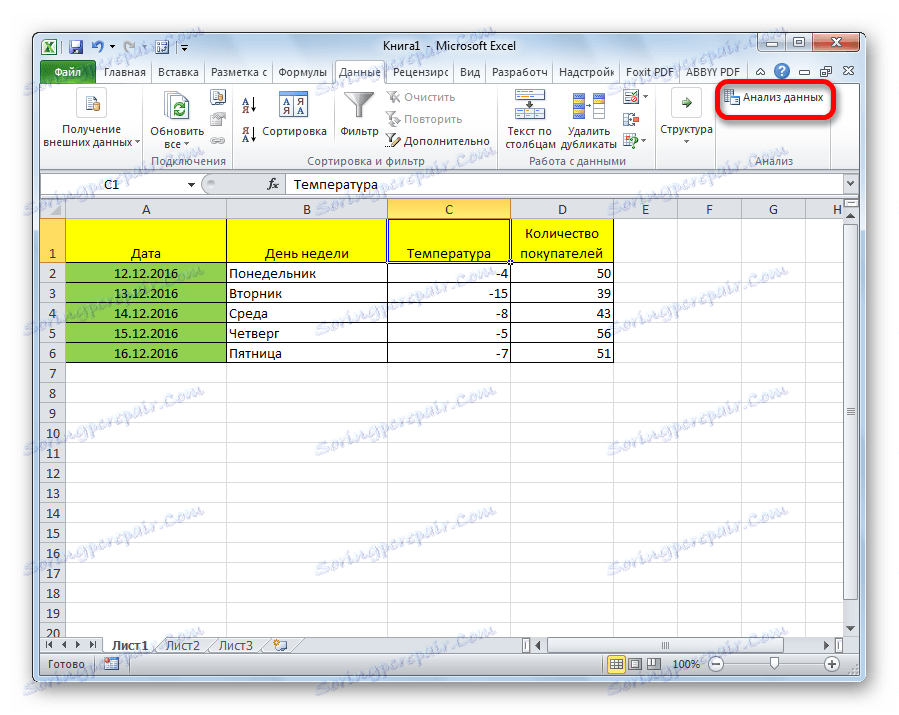
Сега, когато отидем в раздела "Данни" , ще видим нов бутон върху лентата в полето "Анализ" - "Анализ на данните" .

Видове регресионен анализ

Има няколко типа регресии:

• параболична;
• степен;
• логаритмична;
• експоненциално;
• експоненциално;
• хиперболичен;
• линейна регресия.

За изпълнението на последния тип регресионен анализ в Excel ще обсъдим по-подробно по-късно.

Линейна регресия в Excel

По-долу е представена таблицата, която показва средната дневна температура на въздуха на улицата и броя купувачи за съответния работен ден. Нека да разберем с помощта на регресионния анализ точно как климатичните условия под формата на температура на въздуха могат да повлияят на присъствието на търговска институция.

Общото уравнение на линейна регресия е, както следва: У = а0 + а1х1 +…+акхк . В тази формула Y означава променлива, влиянието на факторите, върху които се опитваме да учим. В нашия случай това е броят на купувачите. Стойността на x е различните фактори, които засягат променливата. Параметри а са регресионни коефициенти. Това означава, че те определят значението на този или на този фактор. Индексът k означава общия брой на тези фактори.

1. Кликнете върху бутона "Анализ на данните" . Той се намира в раздела "Начало" в полето "Анализ" .
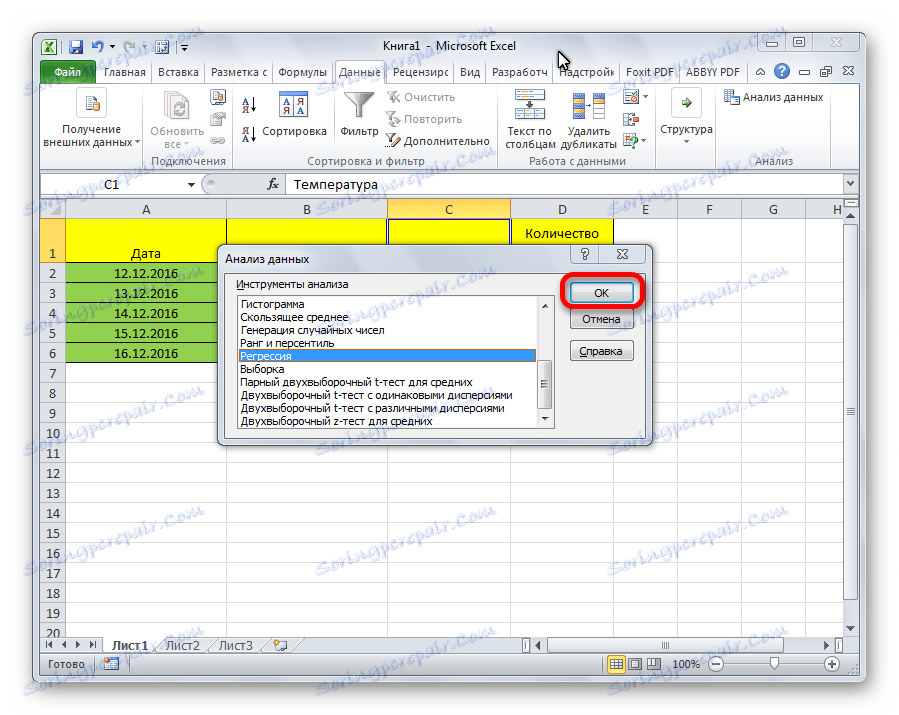
2. Отваря се малък прозорец. В него избираме елемента "Регресия" . Кликнете върху бутона "OK" .
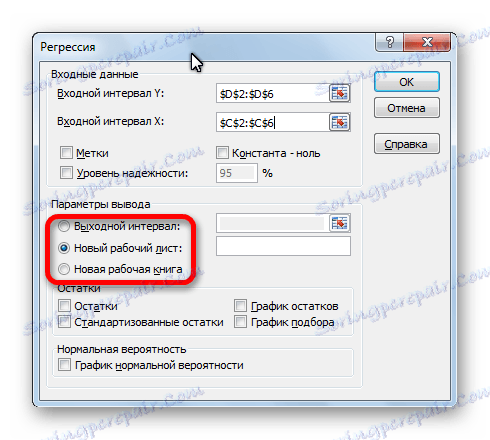
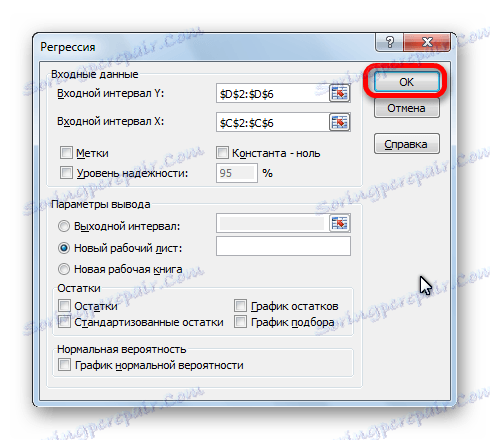
3. Отваря се прозорецът за настройки за регресия. В него задължителните полета са "Интервал на въвеждане Y" и "Интервал на въвеждане X" . Всички останали настройки могат да бъдат оставени по подразбиране.

   В полето "Интервал на въвеждане Y" посочваме адреса на диапазона от клетки, където се намират променливите данни, влиянието на факторите, върху които се опитваме да установим. В нашия случай те ще бъдат клетки в графата "Брой купувачи". Адресът може да бъде въведен ръчно от клавиатурата или просто да изберете необходимата графа. Последният вариант е много по-прост и по-удобен.

   В полето "Интервал на въвеждане X" въвеждаме адреса на диапазона от клетки, където се намират данните на фактора, чието влияние върху променливата, която искаме да установим. Както е посочено по-горе, трябва да установим ефекта на температурата върху броя купувачи и следователно да въведем адреса на клетките в колоната "Температура". Това може да стане по същия начин, както в полето "Брой купувачи".

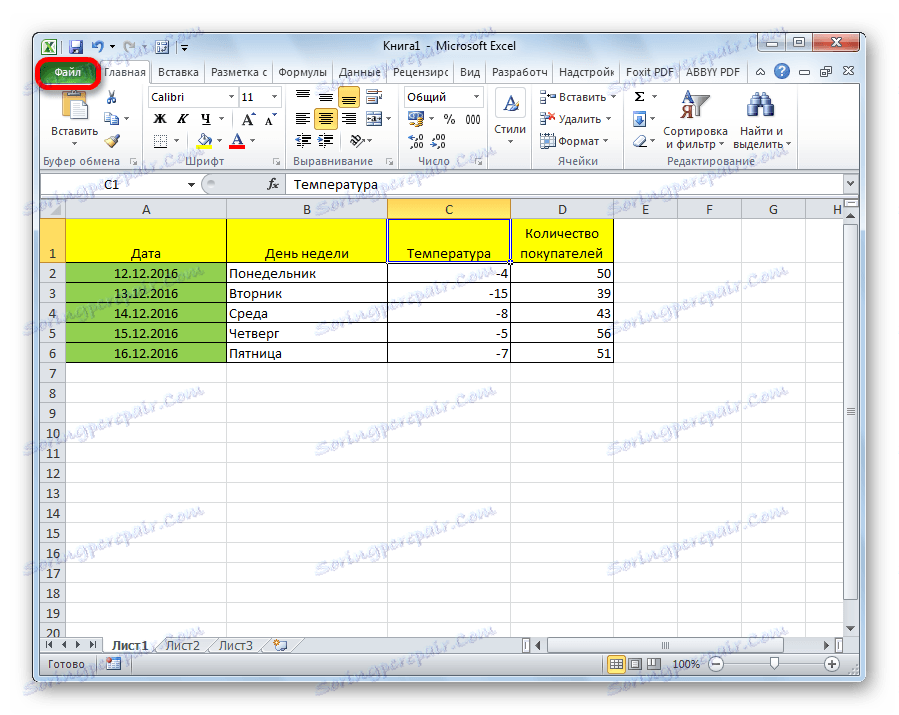
   С помощта на други настройки можете да зададете етикети, ниво на надеждност, постоянна нула, да показвате графика на нормалната вероятност и да изпълнявате други действия. Но в повечето случаи тези настройки не е необходимо да се променят. Единственото нещо, на което трябва да обърнете внимание, е параметрите на изхода. По подразбиране резултатите от анализа се извеждат на друг лист, но с промяна на превключвателя можете да зададете изхода в зададения диапазон на същия лист като таблицата, съдържаща оригиналните данни, или в отделна книга, т.е. в нов файл.

   След като сте задали всички настройки, кликнете върху бутона "OK" .

Анализиране на резултатите от анализа

Резултатите от регресионния анализ се показват под формата на таблица на мястото, посочено в настройките.

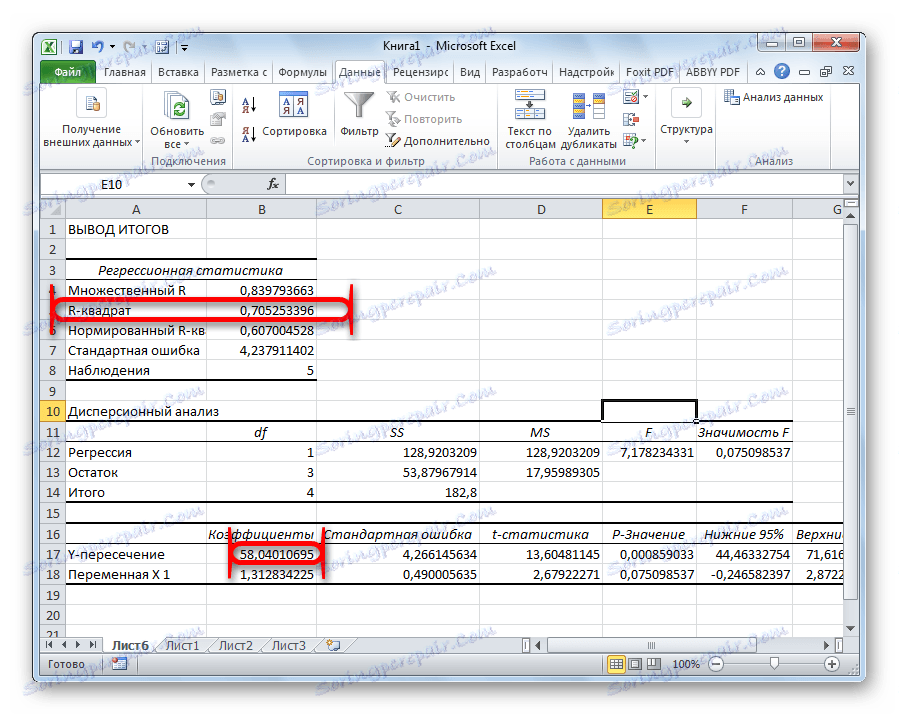
Един от основните индикатори е R-квадрата . Показва качеството на модела. В нашия случай този коефициент е равен на 0.705 или около 70.5%. Това е приемливо ниво на качество. Зависимостта по-малка от 0.5 е лоша.

Друг важен показател се намира в клетката в пресечната точка на линията "Y-пресичане" и в колоната "Коефициенти" . Тя показва коя стойност ще бъде в Y, а в нашия случай това е броят на купувачите, като всички други фактори са равни на нула. В тази таблица тази стойност е 58.04.

Стойността в пресечната точка на графиката "Променлива X1" и "Коефициенти" показва нивото на зависимост на Y от X. В нашия случай това е нивото на зависимостта на броя на клиентите на магазините от температурата. Коефициентът 1.31 е сравнително висок показател за въздействие.

Както можете да видите, с помощта на програмата Microsoft Excel е доста лесно да създадете таблица за регресионни анализи. Но, за да се работи с данните, получени в изхода, и да разберат същността им, само един обучен човек може.

• ← Консолидиране на данни в Microsoft Excel
• Създаване на хистограма в Microsoft Excel →