Прилагане на метода на най-малките квадрати в Excel
Методът на най-малките квадрати е математическа процедура за конструиране на линейно уравнение, което най-точно съответства на набор от две серии от числа. Целта на този метод е да се сведе до минимум общата квадратична грешка. В Excel има инструменти, с които можете да приложите този метод във вашите изчисления. Да видим как е направено.
съдържание
Използване на метода в Excel
Методът на най-малките квадрати (OLS) е математическо описание на зависимостта на една променлива от втората. Тя може да се използва при прогнозиране.
Активиране на добавката за търсене на решение
За да използвате OLS в Excel, трябва да активирате добавката "Find Solution", която е деактивирана по подразбиране.
- Отворете раздела "Файл" .
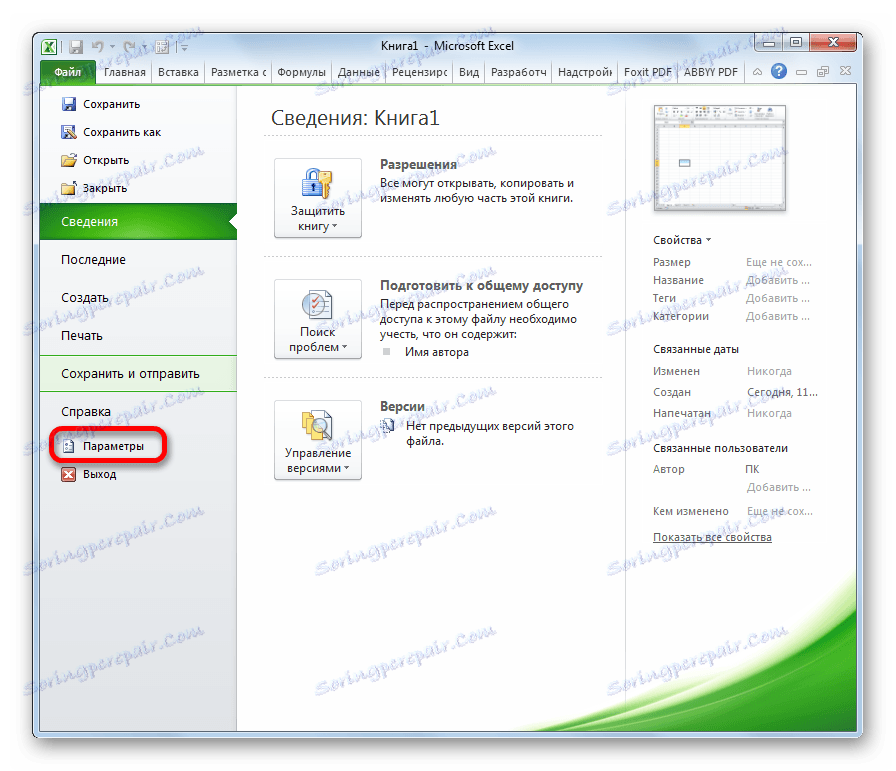
- Кликваме върху името на раздела "Параметри" .
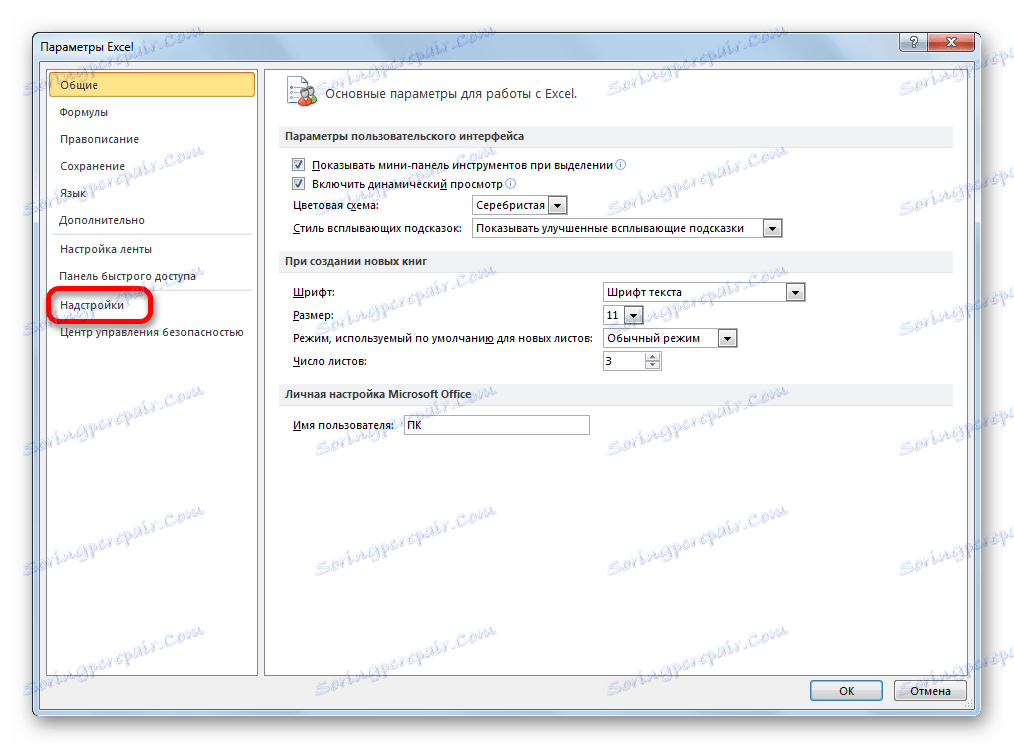
- В отворения прозорец спираме да избираме подраздел "Добавки" .
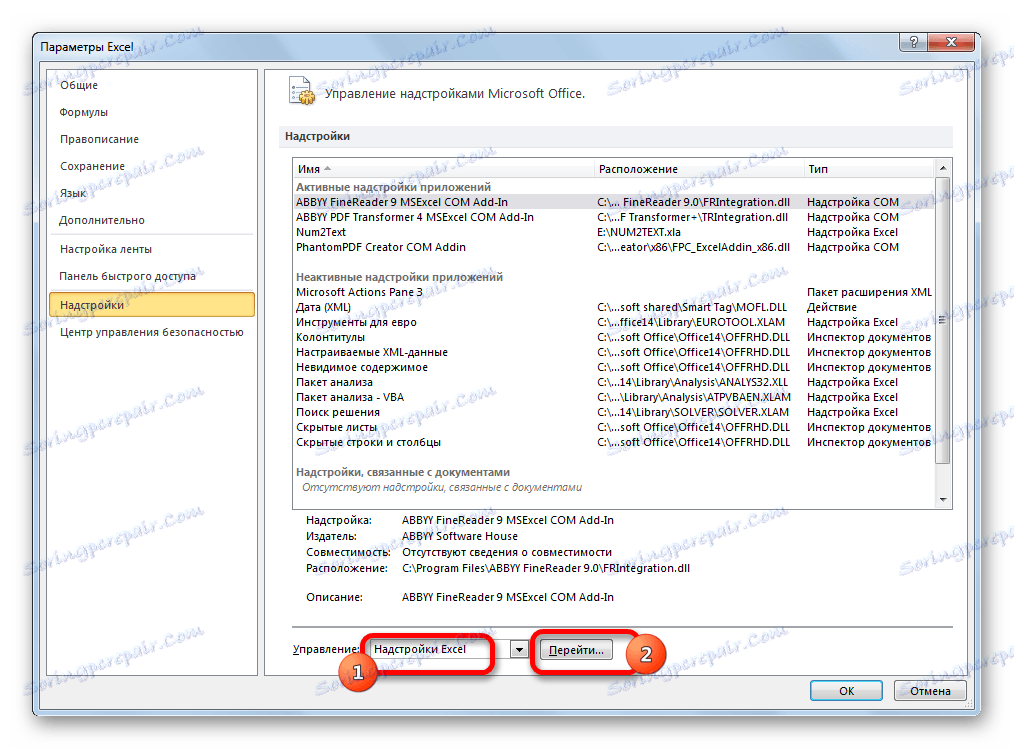
- В блока "Управление" , който се намира в долната част на прозореца, задайте превключвателя на позиция "Добавки в Excel" (ако има различна стойност) и кликнете върху бутона "Отиди ..." .
- Отваря се малък прозорец. Поставяме си отметка за параметъра "Намиране на решения" . Кликнете върху бутона "OK" .
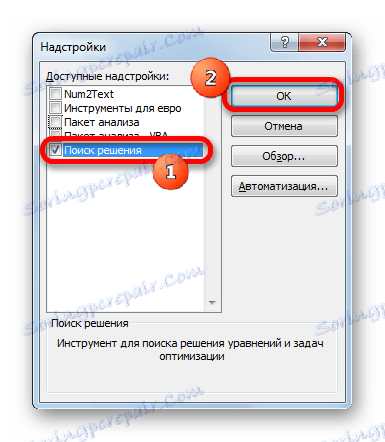
Сега функцията Find Solution in Excel е активирана и нейните инструменти се появяват на лентата.
Урокът: Търсене в разтвор в Excel
Условия на задачите
Нека опишем приложението на OLS на конкретен пример. Имаме два реда числа х и у , чиято последователност е показана на изображението по-долу.
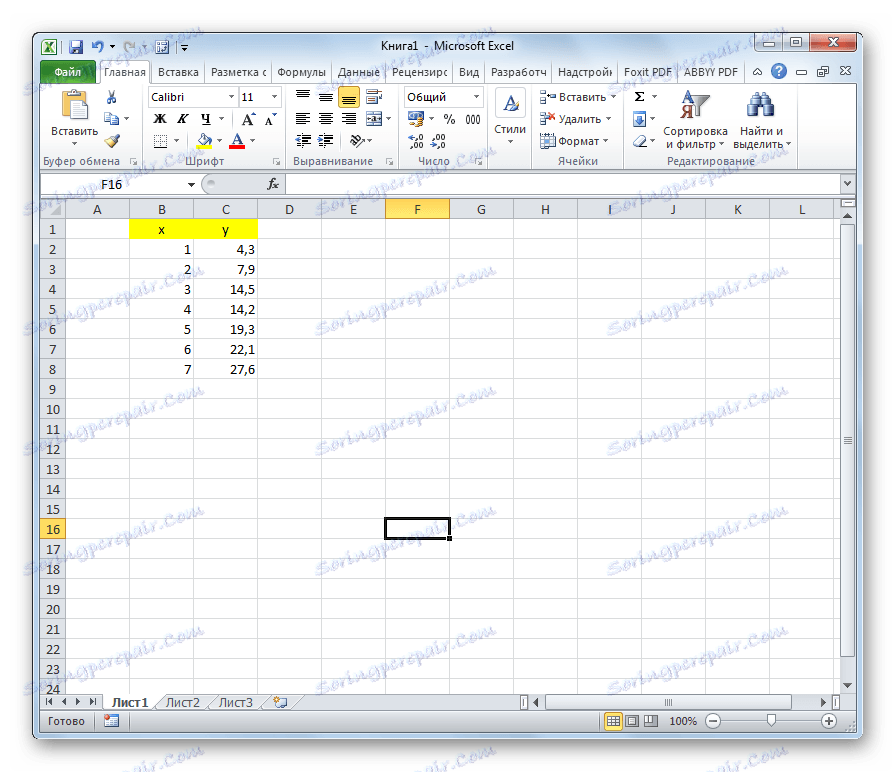
Функцията може най-точно да опише тази зависимост:
y=a+nx
В този случай е известно, че за х = 0, у е също 0 . Следователно, това уравнение може да бъде описано от зависимостта y = nx .
Трябва да намерим минималната сума от квадратите на разликата.
Решението
Нека сега описваме директното прилагане на метода.
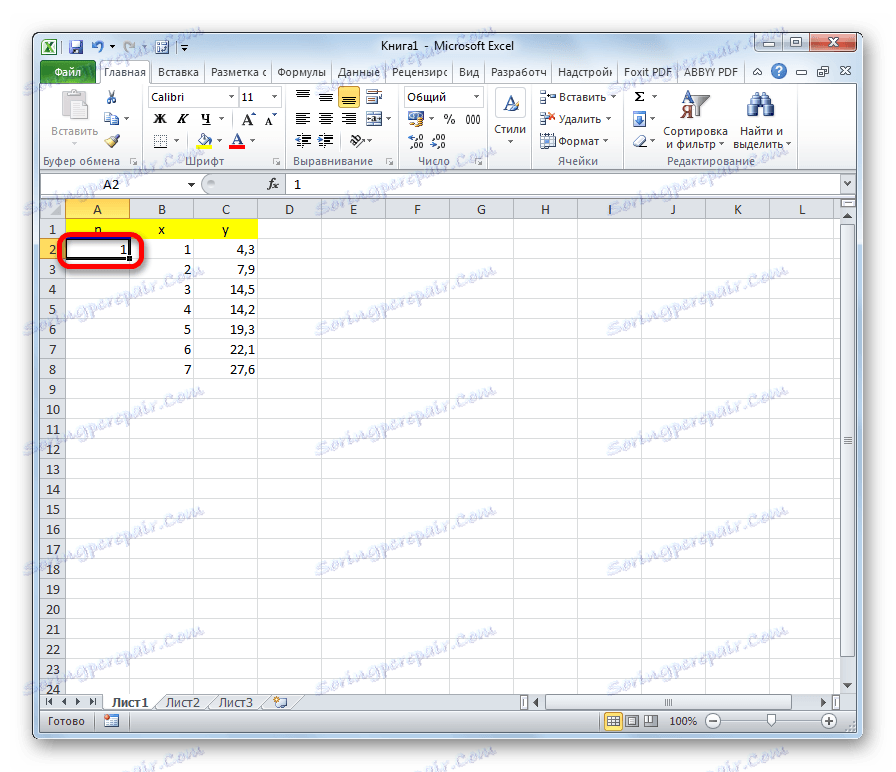
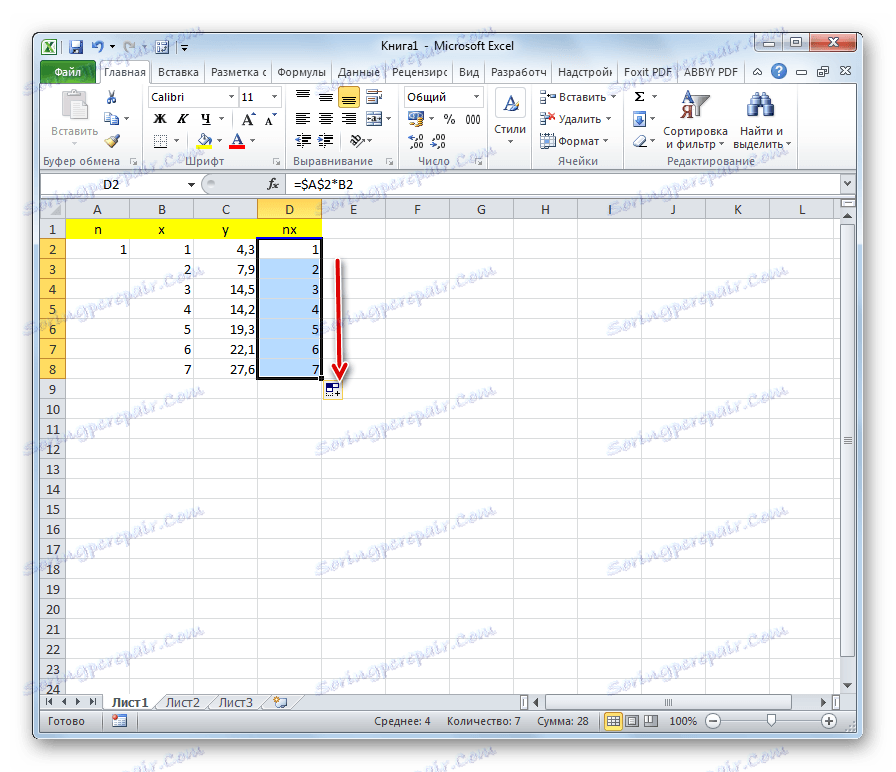
- Вляво от първата стойност на x поставяме числото 1 . Това е приблизителната стойност на първата стойност на коефициента n .
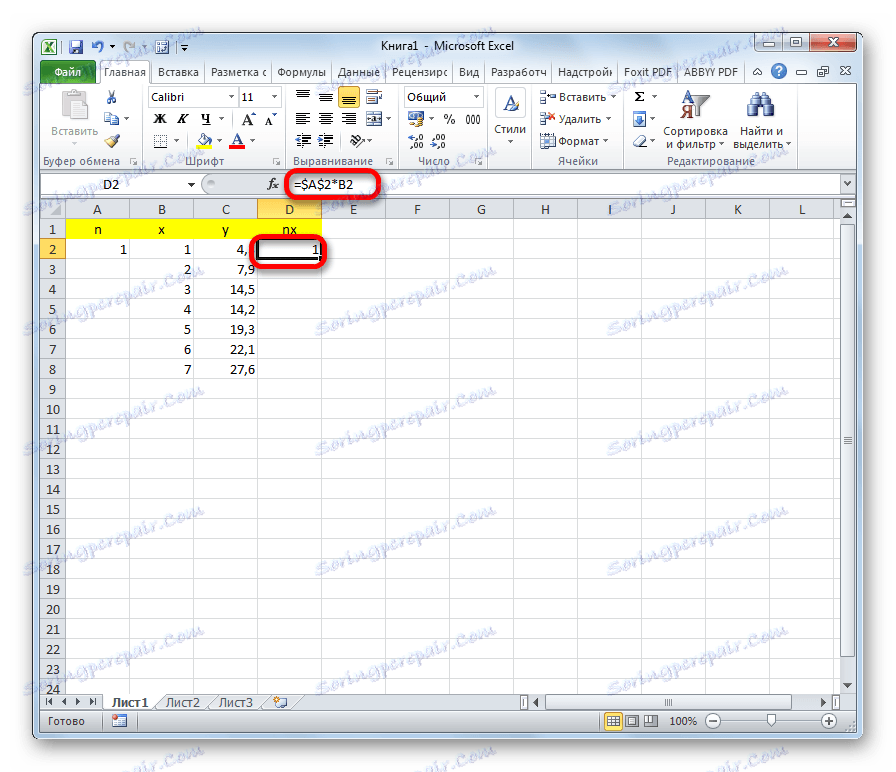
- Вдясно от колоната y добавете още една колона - nx . В първата клетка на тази колона ние начертаваме формулата за умножаване на коефициента n от клетката на първата променлива x . В същото време се прави връзка с полето с коефициент абсолютен , тъй като тази стойност няма да се промени. Кликнете върху бутона Enter .
- използване знак за попълване , копирайте тази формула в целия диапазон на таблицата в колоната по-долу.
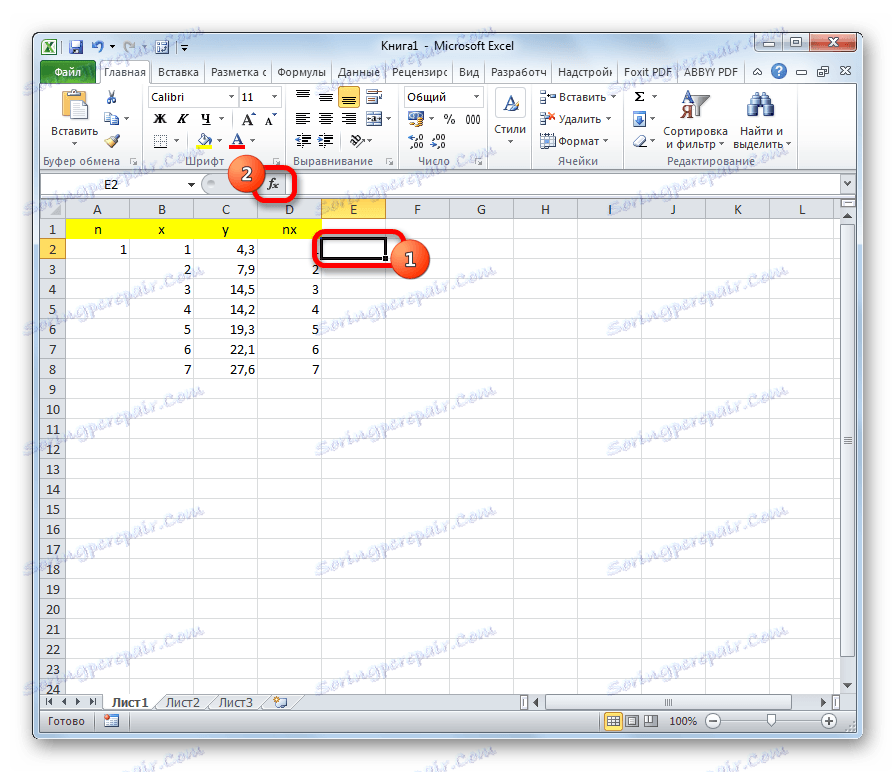
- В отделна клетка изчислете сумата от разликите на квадратите на стойностите на y и nx . За да направите това, кликнете върху бутона "Вмъкване на функция" .
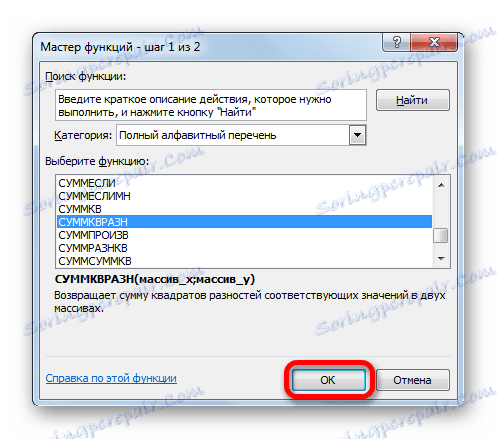
- В отворения "Wizard of functions" търсим вписването "SUMMKVRAZN" . Изберете го и кликнете върху бутона "OK" .
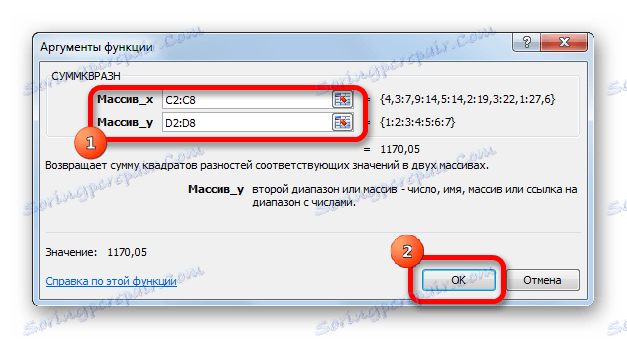
- Отваря прозореца с аргументи. В полето "Array_x" въвеждаме диапазона от клетки на колоната y . В полето "Array_y" влизаме в обхвата на клетките на колоната nx . За да въведете стойности, просто поставете курсора в полето и изберете подходящия диапазон на листа. След въвеждане щракнете върху бутона "OK" .
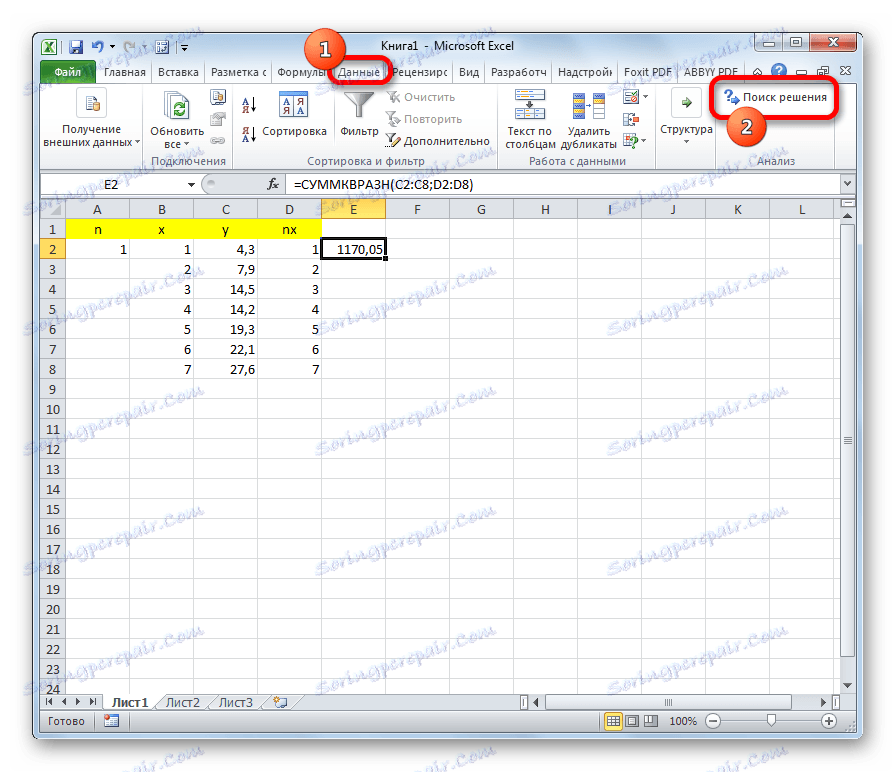
- Отворете раздела "Данни" . На лентата в инструментариума "Анализ" кликнете върху бутона "Намиране на решение" .
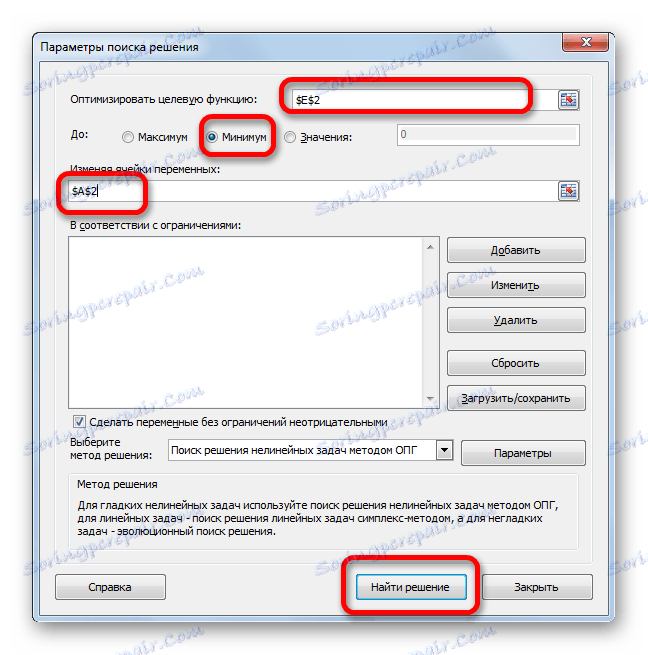
- Отваря се прозорецът с параметри за този инструмент. В полето "Оптимизиране на целевата функция" указваме адреса на клетката с формулата "SUMMKVRAZN" . В параметъра "До" трябва да зададем превключвателя на позиция "Минимална" . В полето "Промяна на клетките" посочваме адреса със стойността на коефициента n . Кликнете върху бутона "Намиране на решение" .
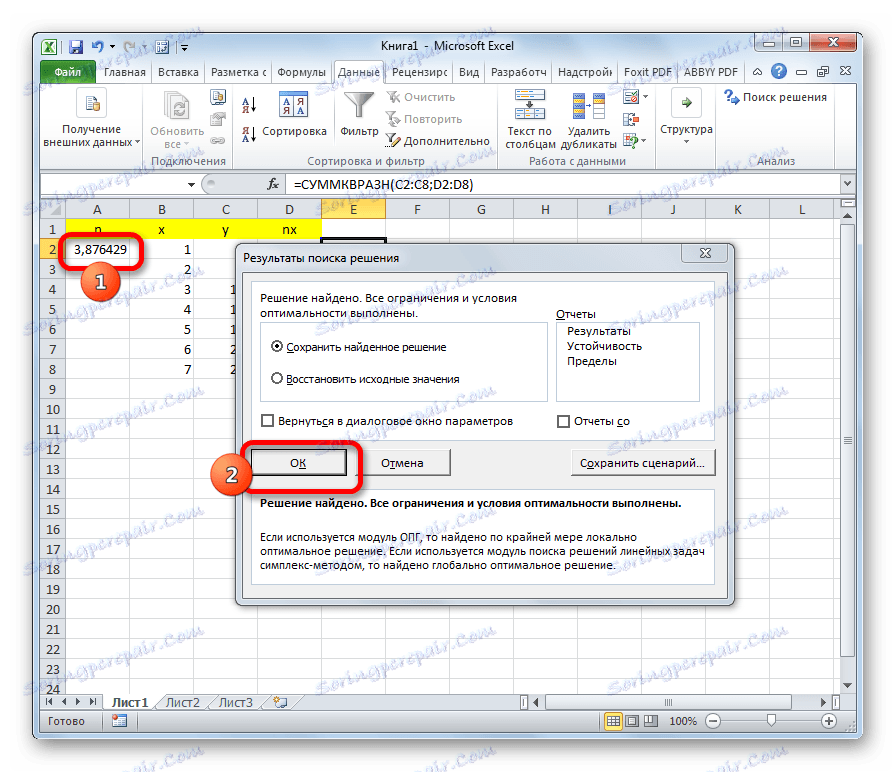
- Решението ще се покаже в клетката на коефициента n . Тази стойност ще бъде най-малкият квадрат на функцията. Ако резултатът удовлетворява потребителя, кликнете върху бутона "OK" в допълнителния прозорец.
Както виждаме, прилагането на метода на най-малките квадрати е доста сложна математическа процедура. Показахме я в действие по най-простия пример и има много по-сложни случаи. Наборът от инструменти на Microsoft Excel обаче има за цел да опрости изчисленията колкото е възможно повече.